
【题目】观察下列等式:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4…
利用你的发现的规律解决下列问题
(1)(a﹣b)(a4+a3b+a2b2+ab3+b4)= (直接填空);
(2)(a﹣b)(an﹣1+an﹣2b+an﹣3b2…+abn﹣2+bn﹣1)= (直接填空);
(3)利用(2)中得出的结论求62019+62018+…+62+6+1的值.
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长为1cm,平移图中的△ABC,使点B移到点B1的位置.
(1)利用方格和直尺画图
①画出平移后的△A1B1C1
②画出AB边上的中线CD;
③画出BC边上的高AH;
(2)线段A1C1与线段AC的位置关系与数量关系为 ;
(3)△A1B1C1的面积为 cm2;△BCD的面积为 cm2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为6的正方形ABCD内部有一点P,BP=4,∠PBC=60°,点Q为正方形边上一动点,且△PBQ是等腰三角形,则符合条件的Q点有__________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD上的E点处,折痕的一端G点在边BC上,折痕的另一端F在AD边上且BG=10时.
(1)证明:EF=EG;
(2)求AF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
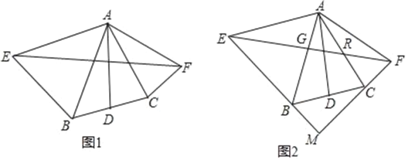
【题目】已知,如图AD为△ABC的中线,分别以AB和AC为一边在△ABC的外部作等腰三角形ABE和等腰三角形ACF,且AE=AB,AF=AC,连接EF,∠EAF+∠BAC=180°
(1)如图1,若∠ABE=63°,∠BAC=45°,求∠FAC的度数;
(2)如图1请探究线段EF和线段AD有何数量关系?并证明你的结论;
(3)如图2,设EF交AB于点G,交AC于点R,延长FC,EB交于点M,若点G为线段EF的中点,且∠BAE=70°,请探究∠ACB和∠CAF的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(
的图象如图所示,以下结论:①abc>0;②4ac<b2;③2a+b>0;④其顶点坐标为(![]() ,﹣2);⑤当x<
,﹣2);⑤当x<![]() 时,y随x的增大而减小;⑥a+b+c>0正确的有( )
时,y随x的增大而减小;⑥a+b+c>0正确的有( )

A. 3个 B. 4个 C. 5个 D. 6个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一元二次方程![]() ,有下列说法:
,有下列说法:
①若![]() ,则方程
,则方程![]() 必有一个根为1;
必有一个根为1;
②若方程![]() 有两个不相等的实根,则方程
有两个不相等的实根,则方程![]() 必有两个不相等的实根;
必有两个不相等的实根;
③若![]() 是方程
是方程![]() 的一个根,则一定有
的一个根,则一定有![]() 成立;
成立;
④若![]() 是一元二次方程
是一元二次方程![]() 的根,则
的根,则![]() .
.
其中正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】再读教材:宽与长的比是![]() (约为
(约为![]() )的矩形叫做黄金矩形,黄金矩形给我们以协调、匀称的美感.世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为
)的矩形叫做黄金矩形,黄金矩形给我们以协调、匀称的美感.世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计,下面我们用宽为![]() 的矩形纸片折叠黄金矩形(提示:
的矩形纸片折叠黄金矩形(提示:![]() )
)
第一步:在矩形纸片一端利用图①的方法折出一个正方形,然后把纸片展平.

第二步:如图②,把这个正方形折成两个相等的矩形,再把纸片展平.

第三步:折出内侧矩形的对角线![]() ,并把
,并把![]() 折到图③中所示的
折到图③中所示的![]() 处.
处.

第四步:展平纸片,按照所得的点![]() 折出
折出![]() 使
使![]() 则图④中就会出现黄金矩形.
则图④中就会出现黄金矩形.

问题解决:
(1)图③中![]() _ (保留根号);
_ (保留根号);
(2)如图③,判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(3)请写出图④中所有的黄金矩形,并选择其中一个说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com