
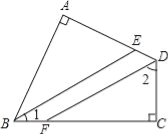
【题目】四边形ABCD中,∠A=∠C=90°,BE、DF分别是∠ABC、∠ADC的平分线.求证:
(1)、∠1+∠2=90°;(2)、BE∥DF.
【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、根据角平分线的性质得出∠1=∠ABE,∠2=∠ADF。根据四边形内角和定理可得∠ABC+∠ADC=180°,即2(∠1+∠2)=180°,从而得出答案;(2)、根据三角形内角和定理可得∠DFC+∠2=90°,结合第一题的结论得出∠1=∠DFC,从而得出答案.
试题解析:(1)、∵BE,DF分别是∠ABC,∠ADC的平分线, ∴∠1=∠ABE,∠2=∠ADF,
∵∠A=∠C=90°, ∴∠ABC+∠ADC=180°, ∴2(∠1+∠2)=180°, ∴∠1+∠2=90°;
(2)、在△FCD中,∵∠C=90°, ∴∠DFC+∠2=90°, ∵∠1+∠2=90°,
∴∠1=∠DFC, ∴BE∥DF.


科目:初中数学 来源: 题型:
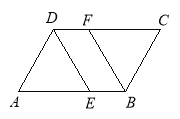
【题目】如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于点E,BF平分∠ABC,交CD于点F.
(1)、求证:DE=BF;(2)、连接EF,写出图中所有的全等三角形.(不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( ).
A. 对角线互相平分的四边形为平行四边形
B. 两组对角分别相等的四边形为平行四边形
C. 一组对边平行且相等的四边形是平行四边形
D. 一组对边平行,另一组对边相等的四边形是平行四边形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学家歌德巴赫通过研究下面一系列等式,作出了一个著名的猜想.
4=2+2; 12=5+7;
6=3+3; 14=3+11=7+7;
8=3+5; 16=3+13=5+11;
10=3+7=5+5 18=5+13=7+11;
…
通过这组等式,你发现的规律是 (请用文字语言表达).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com