
分析 根据方程有两个相等的实数根可得△=0,即4(b-a)2-4(ab-2b)(2a-ab)=0,整理后可得[(a+b)-ab]2=0,从而可知a+b=ab,即可得答案.
解答 解:依题意,△=4(b-a)2-4(ab-2b)(2a-ab)=0
即:(a+b)2-4ab+(ab-2b)(ab-2a)=0
(a+b)2-4ab+[a2b2-2ab(a+b)+4ab]=0
(a+b)2+a2b2-2ab(a+b)=0
[(a+b)-ab]2=0
∴a+b=ab,
则$\frac{1}{a}$+$\frac{1}{b}$=1,
故答案为:1.
点评 本题主要考查一元二次方程根的判别式,根据根的判别式为0得出a、b间的关系式是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
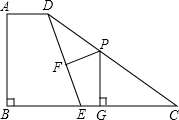 已知,如图,在四边形ABCD中,AD∥BC,∠B=90°,点E在BC上,∠CDE=∠C,点P在CD上,PF⊥DE、PG⊥BC,点F、G为垂足,求证.PF+PG=AB.
已知,如图,在四边形ABCD中,AD∥BC,∠B=90°,点E在BC上,∠CDE=∠C,点P在CD上,PF⊥DE、PG⊥BC,点F、G为垂足,求证.PF+PG=AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星 期 | 一 | 二 | 三 | 四 | 五 |
| 收盘价涨跌值/元 | -1.4 | +0.5 | +1.1 | -0.6 | +0.4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com