
 如图,这是一个4×7的正方形网格,则图中一共有60个正方形,一共有280个长方形.
如图,这是一个4×7的正方形网格,则图中一共有60个正方形,一共有280个长方形. 分析 (1)先从1×1开始数起,1×1的正方形有7×4=28个;2×2的正方形有6×3=18个;3×3的正方形有5×2=10个,4×4的正方形有4×1=4个,由此再利用加法原理即可解答;
(2)先从1×2开始数起,分别找出1×3;1×4;1×5;1×6;1×7;2×3;2×4;2×5;2×6;2×7;3×4;3×5;3×6;3×7;4×5;4×6;4×7的正方形各有多少个,再把它们与(1)中的正方形的个数加起来即可解决问题.也可以根据长边的线段上有8个点,得出线段的条数为28条,短边的线段上有5个点,得出线段的条数为10条,长方形的个数为28×10=280(个).
解答 解:①因为:1×1的正方形有7×4=28个,
2×2的正方形有6×3=18个,
3×3的正方形有5×2=10个,
4×4的正方形有4×1=4个,
所以,正方形有28+18+10+4=60(个),
②1×2的长方形有7×3+4×6=45个,1×3的长方形有:7×2+4×5=34个,
1×4的长方形有:7×1+4×4=23个,
1×5的长方形有:4×3=12个,
1×6的长方形有:4×2=8个,
1×7的长方形有:4×1=4个,
2×3的长方形有6×2+3×5=27个,
2×4的长方形有6×1+3×4=18个,
2×5的长方形有:3×3=9个,
2×6的长方形有:3×2=6,
2×7的长方形有:3×1=3,
3×4的长方形有:5×1+2×4=13个,
3×5的长方形有:2×3=6个,
3×6的长方形有:2×2=4,
3×7的长方形有:2×1=2,
4×5的长方形有:3×1=3,
4×6的长方形有:2×1=2,
4×7的长方形有:1,
45+34+23+12+8+4+27+18+9+6+3+13+6+4+2+3+2+1=220(个),220+60=280(个);
所以4×7的正方形网格,一共有60个正方形,一共有280个长方形.
故答案为:60;280.
点评 本题是认识平面图形,考查了正方形和长方形的计数,在图形的计数时,应注重一定的顺序计数,做到不遗漏,不重复.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:选择题
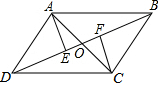 如图,已知AB∥CD,AD∥BC,AC与BD交于点O,AE⊥BD于点E,CF⊥BD于点F,那么图中全等的三角形有( )
如图,已知AB∥CD,AD∥BC,AC与BD交于点O,AE⊥BD于点E,CF⊥BD于点F,那么图中全等的三角形有( )| A. | 5对 | B. | 6对 | C. | 7对 | D. | 8对 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ a2c | B. | $\frac{1}{4}$ ac | C. | $\frac{9}{4}$ a2c | D. | $\frac{9}{4}$ ac |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
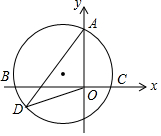 如图,在直角坐标系中,已知点A(0,4),B(-4,0),C(2,0),过A,B,C作外接圆,D为圆上一动点,求$\sqrt{5}$DO+DA的最小值.
如图,在直角坐标系中,已知点A(0,4),B(-4,0),C(2,0),过A,B,C作外接圆,D为圆上一动点,求$\sqrt{5}$DO+DA的最小值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≤1 | B. | -1≤a≤1 | C. | a≤-1 | D. | -1≤a≤0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com