
分析 (1)由于m≠0,则计算判别式的值得到△=1,从而可判断方程总有两个不相等的实数根;
(2)先利用求根公式得到x1=-1,x2=$\frac{1}{m}$-1,然后利用有理数的整除性确定整数m的值.
解答 (1)证明:∵m≠0,
∴方程为一元二次方程,
∵△=(2m-1)2-4m(m-1)=1>0,
∴此方程总有两个不相等的实数根;
(2)∵x=$\frac{-(2m-1)±1}{2m}$,
∴x1=-1,x2=$\frac{1}{m}$-1,
∵方程的两个实数根都是整数,且m是整数,
∴m=1或m=-1.
点评 本题考查了根的判别式:一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:当△>0时,方程有两个不相等的实数根;当△=0时,方程有两个相等的实数根;当△<0时,方程无实数根.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:解答题
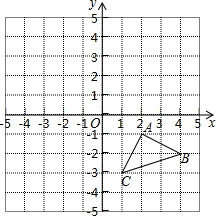 三角形ABC的三个顶点坐标分别为A(2,-1),B(4,-2),C(1,-3),将三角形ABC平移至三角形A1B1C1的位置,点A、B、C对应的点分别为A1,B1,C1,已知点A1的坐标是(-2,3).
三角形ABC的三个顶点坐标分别为A(2,-1),B(4,-2),C(1,-3),将三角形ABC平移至三角形A1B1C1的位置,点A、B、C对应的点分别为A1,B1,C1,已知点A1的坐标是(-2,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
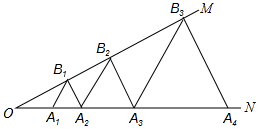 如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2017=22016.
如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,从左起第1个等边三角形的边长记为a1,第2个等边三角形的边长记为a2,以此类推.若OA1=1,则a2017=22016.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 填空完成推理过程:
填空完成推理过程:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com