
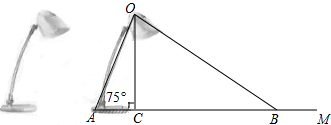
 ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćAµÄ×ų±źĪŖ£Ø3£¬0£©£¬BĪŖÖ±Ļßy=$\frac{\sqrt{3}}{3}$xÉĻµÄŅ»øö¶Æµć£¬ŃÓ³¤ABÖĮC£¬Ź¹µĆAB=BC£¬¹żµćC×÷CD”ĶxÖįÓŚµćD£¬½»Ö±ĻßOBÓŚµćF£¬¹żµćA×÷AE”ĪOB£¬½»Ö±ĻßCDÓŚµćE£®
ČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćAµÄ×ų±źĪŖ£Ø3£¬0£©£¬BĪŖÖ±Ļßy=$\frac{\sqrt{3}}{3}$xÉĻµÄŅ»øö¶Æµć£¬ŃÓ³¤ABÖĮC£¬Ź¹µĆAB=BC£¬¹żµćC×÷CD”ĶxÖįÓŚµćD£¬½»Ö±ĻßOBÓŚµćF£¬¹żµćA×÷AE”ĪOB£¬½»Ö±ĻßCDÓŚµćE£®·ÖĪö £Ø1£©øł¾ŻĮ½Ö±ĻßĘ½ŠŠkĻąĶ¬£¬ĄūÓĆ“ż¶ØĻµŹż·Ø¼“æɽā¾öĪŹĢā£»
£Ø2£©ŌŚµćBŌĖ¶Æ¹ż³ĢÖŠ£¬Ļ߶ĪCFµÄ³¤²»·¢Éś±ä»Æ£®¹żµćA×÷AG”ĶOA£¬½»OBÓŚG£®Ö»ŅŖÖ¤Ć÷”÷ABG”Õ”÷CBF£¬¼“æÉĶĘ³öCF=AG=$\sqrt{3}$£»
£Ø3£©Ēó³öAD”¢CD£¬øł¾Żtan”ĻCAD=$\frac{CD}{AD}$¼ĘĖć¼“æÉ£»
£Ø4£©“ęŌŚ£®ÓÉAB=BC£¬BF”ĪAEæÉÖŖBFŹĒ”÷AECµÄÖŠĪ»Ļߣ¬ĶĘ³öAE=2BF£¬EF=CF=$\sqrt{3}$£¬·ÖČżÖÖĒéŠĪĢÖĀŪ¼“æÉ£ŗ¢ŁČōBE”ĶAE£¬ČēĶ¼1ÖŠ£¬ŌņBE”ĶBF£®¢ŚČōAB”ĶBE£¬ČēĶ¼2ÖŠ£®¢ŪČōAB”ĶAE£¬ČēĶ¼3ÖŠ£®·Ö±šĒó½ā¼“æÉ£»
½ā“š ½ā£ŗ£Ø1£©”ßAE”ĪOB£¬Ö±ĻßOBµÄ½āĪöŹ½ĪŖy=$\frac{\sqrt{3}}{3}$x£¬
”ąæÉŅŌ¼ŁÉčÖ±ĻßAEµÄ½āĪöŹ½ĪŖy=$\frac{\sqrt{3}}{3}$x+b£¬
°ŃA£Ø3£¬0£©“śČėµĆµ½b=-$\sqrt{3}$£¬
”ąÖ±ĻßAEµÄ½āĪöŹ½ĪŖy=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$£®
£Ø2£©ŌŚµćBŌĖ¶Æ¹ż³ĢÖŠ£¬Ļ߶ĪCFµÄ³¤²»·¢Éś±ä»Æ£®
¹żµćA×÷AG”ĶOA£¬½»OBÓŚG£®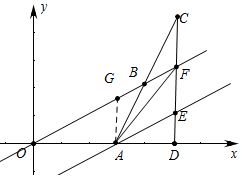
”ßµćA£Ø3£¬0£©£¬
”ąµćGµÄŗį×ų±źĪŖ3£¬
½«x=3“śČėy=$\frac{\sqrt{3}}{3}$x£¬µĆµ½y=$\sqrt{3}$£¬
”ąAG=$\sqrt{3}$£¬
”ßAG”ĪCD£¬BĪŖACÖŠµć£¬
”ą”ĻAGB=”ĻCFB£¬”ĻBAG=”ĻBCF£¬AB=BC£¬
”ą”÷ABG”Õ”÷CBF£¬
”ąCF=AG=$\sqrt{3}$£®
£Ø3£©ÓÉ£Ø2£©æÉÖŖtan”ĻGOA=$\frac{\sqrt{3}}{3}$£¬
”ą”ĻEAD=”ĻGOA=30”ć£¬
”ßEF=AG=AD=CF=$\sqrt{3}$£¬
”ąED=AD•tan30”ć=1£¬
”ąCD=1+2$\sqrt{3}$
”ątan”ĻCAD=$\frac{CD}{AD}$=$\frac{1+2\sqrt{3}}{\sqrt{3}}$=$\frac{6+\sqrt{3}}{3}$£®
£Ø4£©“ęŌŚ£®
ÓÉAB=BC£¬BF”ĪAEæÉÖŖBFŹĒ”÷AECµÄÖŠĪ»Ļߣ¬
”ąAE=2BF£¬EF=CF=$\sqrt{3}$£¬
¢ŁČōBE”ĶAE£¬ČēĶ¼1ÖŠ£¬ŌņBE”ĶBF£¬CF=EF=$\sqrt{3}$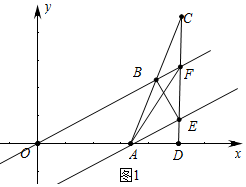
”ß”ĻBFE=60”ć£¬
”ąBF=EF•cos60”ć=$\frac{\sqrt{3}}{2}$£¬
”ąAE=$\sqrt{3}$£¬
ŌŚRt”÷ADEÖŠ£¬ED=$\frac{\sqrt{3}}{2}$£¬AD=$\frac{3}{2}$£¬“ĖŹ±E£Ø$\frac{9}{2}$£¬$\frac{\sqrt{3}}{2}$£©£®
¢ŚČōAB”ĶBE£¬ČēĶ¼2ÖŠ£¬CF=EF=$\sqrt{3}$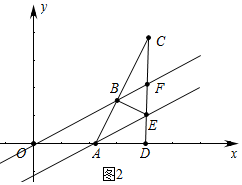
Ņ×ÖŖBF=$\frac{1}{2}$CE=$\sqrt{3}$£¬
”ąAE=2$\sqrt{3}$£¬
ŌŚRt”÷ADEÖŠ£¬DE=$\sqrt{3}$£¬AD=3£¬“ĖŹ±E£Ø6£¬$\sqrt{3}$£©£®
¢ŪČōAB”ĶAE£¬ČēĶ¼3ÖŠ£¬CF=$\sqrt{3}$£¬”ĻC=30”ć£¬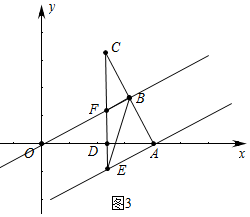
Ņ×ÖŖBF=$\frac{\sqrt{3}}{2}$£¬
”ąAE=$\sqrt{3}$£¬
ŌŚRt”÷ADEÖŠ£¬ED=$\frac{\sqrt{3}}{2}$£¬AD=$\frac{3}{2}$£¬“ĖŹ±E£Ø$\frac{3}{2}$£¬-$\frac{\sqrt{3}}{2}$£©£¬
×ŪÉĻĖłŹö£¬Āś×ćĢõ¼žµÄµćE×ų±źĪŖ£Ø$\frac{9}{2}$£¬$\frac{\sqrt{3}}{2}$£©»ņ£Ø6£¬$\sqrt{3}$£©»ņ£Ø$\frac{3}{2}$£¬-$\frac{\sqrt{3}}{2}$£©£®
µćĘĄ ±¾Ģāæ¼²éŅ»“ĪŗÆŹżµÄÓ¦ÓĆ”¢Č«µČČż½ĒŠĪµÄÅŠ¶ØŗĶŠŌÖŹ”¢Čń½ĒČż½ĒŗÆŹż”¢½āÖ±½ĒČż½ĒŠĪ”¢Ö±½ĒČż½ĒŠĪ30¶Č½ĒŠŌÖŹµČÖŖŹ¶£¬½āĢāµÄ¹Ų¼üŹĒĮé»īŌĖÓĆĖłŃ§ÖŖŹ¶½ā¾öĪŹĢā£¬Ń§»įÓĆ·ÖĄąĢÖĀŪµÄĖ¼ĻėĖ¼æ¼ĪŹĢā£¬ŹōÓŚÖŠæ¼Ń¹ÖįĢā£®


 ÖŠæ¼½ā¶Įæ¼µć¾«Į·ĻµĮŠ“š°ø
ÖŠæ¼½ā¶Įæ¼µć¾«Į·ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
 Ņ»ĮŠæģ³µ“Ó¼×µŲŹ»ĶłŅŅµŲ£¬Ņ»ĮŠĀż³µŃŲĶ¬Ņ»Ģõ¹«Ā·“ÓŅŅµŲŹ»Ķł¼×µŲ£¬Į½³µĶ¬Ź±³ö·¢£¬ÉčĀż³µŠŠŹ»µÄŹ±¼äĪŖx£Øµ„Ī»£ŗh£©£¬Į½³µÖ®¼äµÄ¾ąĄėĪŖy£Øµ„Ī»£ŗkm£©£¬Ķ¼ÖŠµÄÕŪĻß±ķŹ¾yÓėxÖ®¼äµÄŗÆŹż¹ŲĻµ£®øł¾ŻĶ¼Ļó½ā“šĻĀĮŠĪŹĢā£ŗ
Ņ»ĮŠæģ³µ“Ó¼×µŲŹ»ĶłŅŅµŲ£¬Ņ»ĮŠĀż³µŃŲĶ¬Ņ»Ģõ¹«Ā·“ÓŅŅµŲŹ»Ķł¼×µŲ£¬Į½³µĶ¬Ź±³ö·¢£¬ÉčĀż³µŠŠŹ»µÄŹ±¼äĪŖx£Øµ„Ī»£ŗh£©£¬Į½³µÖ®¼äµÄ¾ąĄėĪŖy£Øµ„Ī»£ŗkm£©£¬Ķ¼ÖŠµÄÕŪĻß±ķŹ¾yÓėxÖ®¼äµÄŗÆŹż¹ŲĻµ£®øł¾ŻĶ¼Ļó½ā“šĻĀĮŠĪŹĢā£ŗ²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
| A | B | |
| ½ų¼Ū£ØĶņŌŖ/Ģ×£© | 1.5 | 1.2 |
| ŹŪ¼Ū£ØĶņŌŖ/Ģ×£© | 1.65 | 1.4 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
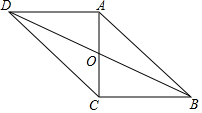 ČēĶ¼£¬ŌŚ?ABCDÖŠ£¬¶Ō½ĒĻßAC”¢BD½»ÓŚµćO£¬AC”ĶBC£¬ĒŅ?ABCDµÄÖܳ¤ĪŖ36£¬”÷OCDµÄÖܳ¤±Č”÷OBCµÄÖܳ¤“ó2£®
ČēĶ¼£¬ŌŚ?ABCDÖŠ£¬¶Ō½ĒĻßAC”¢BD½»ÓŚµćO£¬AC”ĶBC£¬ĒŅ?ABCDµÄÖܳ¤ĪŖ36£¬”÷OCDµÄÖܳ¤±Č”÷OBCµÄÖܳ¤“ó2£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
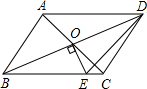 ČēĶ¼£¬ŅŃÖŖ?ABCDµÄ¶Ō½ĒĻß½»ÓŚµćO£¬ĒŅAD”ŁCD£¬¹żO×÷OE”ĶBD½»BCÓŚEµć£¬Čō”÷CDEµÄÖܳ¤ŹĒ8£¬Ōņ?ABCDµÄÖܳ¤ĪŖ16£®
ČēĶ¼£¬ŅŃÖŖ?ABCDµÄ¶Ō½ĒĻß½»ÓŚµćO£¬ĒŅAD”ŁCD£¬¹żO×÷OE”ĶBD½»BCÓŚEµć£¬Čō”÷CDEµÄÖܳ¤ŹĒ8£¬Ōņ?ABCDµÄÖܳ¤ĪŖ16£®²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com