
【题目】在![]() 中,
中,![]() ,
,![]() ,以边
,以边![]() 的中点
的中点![]() 为圆心,作半圆与
为圆心,作半圆与![]() 相切,点
相切,点![]() 分别是边
分别是边![]() 和半圆上的动点,连接
和半圆上的动点,连接![]() ,则
,则![]() 长的最大值与最小值的和是__________.
长的最大值与最小值的和是__________.

【答案】9
【解析】
如图,设O与AC相切于点E,连接OE,作OP1⊥BC垂足为P1交O于Q1,此时垂线段OP1最短,P1Q1最小为OP1-OQ1,当Q2在AB边上时,P2与B重合时,P2Q2最大,即可得出答案.
如图所示:
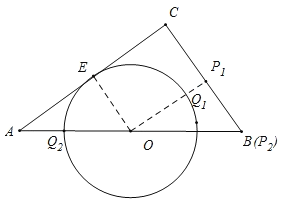
设O与AC相切于点E,连接OE,作OP1⊥BC垂足为P1交 O于Q1,
此时垂线段OP1最短,最小值为OP1-OQ1,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵AO=BO,
∴![]() ,
,
同理可求OE=3,
即![]() ,
,
∴PQ最小值P1Q1=O P1-OQ1=1,
如图,当在AB边上时,与B重合时,P2Q2经过圆心,
∵经过圆心的弦最长,
∴PQ最小值P2Q2=O B-OQ2=3+5=8,
∴PQ长的最大值与最小值的和是1+8=9.
故答案为:9.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.

(1)求证:△ADC≌△CEB.
(2)AD=6cm,DE=4cm,求BE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在正方形网格中有一个△ABC,按要求进行下列作图(只能借助于网格):
(1)画出△ABC中BC边上的高AD;
(2)画出先将△ABC向右平移6格,再向上平移3格后的△A1B1C1;
(3)画一个△BCP(要求各顶点在格点上,P不与A点重合),使其面积等于△ABC的面积.并回答,满足这样条件的点P共________个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC外作射线AD,使得AD和AC在直线AB的两侧,∠BAD=α(0°<α<180°),点B关于直线AD的对称点为P,连接PB,PC.
(1)依题意补全图1;
(2)在图1中,求△BPC的度数;
(3)直接写出使得△PBC是等腰三角形的α的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内,△ABC和△ABD如图①放置,其中AB=BD.
小明做了如下操作:
将△ABC绕着边AC的中点旋转180°得到△CEA,将△ABD绕着边AD的中点旋转180°得到△DFA,如图②,请完成下列问题:
(1)试猜想四边形ABDF是什么特殊四边形,并说明理由;
(2)连接EF,CD,如图③,求证:四边形CDEF是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
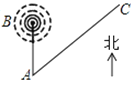
【题目】城市![]() 的正北方向
的正北方向![]() 的
的![]() 处,有一无线电信号发射塔.已知,该发射塔发射的无线电信号的有效半径为
处,有一无线电信号发射塔.已知,该发射塔发射的无线电信号的有效半径为![]() ,
,![]() 是一条直达
是一条直达![]() 城的公路,从
城的公路,从![]() 城发往
城发往![]() 城的班车速度为
城的班车速度为![]() .
.
(1)当班车从![]() 城出发开往
城出发开往![]() 城时,某人立即打开无线电收音机,班车行驶了
城时,某人立即打开无线电收音机,班车行驶了![]() 的时候接收信号最强.此时,班车到发射塔的距离是多少千米?(离发射塔越近,信号越强)
的时候接收信号最强.此时,班车到发射塔的距离是多少千米?(离发射塔越近,信号越强)
(2)班车从![]() 城到
城到![]() 城共行驶了
城共行驶了![]() ,请你判断到
,请你判断到![]() 城后还能接收到信号吗?请说明理由.
城后还能接收到信号吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B,C三点是同一个平面直角坐标系内不同的三点,A点在坐标轴上,点A向左平移3个单位长度,再向上平移2个单位长度就到了B点;直线BC∥y轴,C点的横坐标、纵坐标互为相反数,且点B和点C到x轴的距离相等.则A点的坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() 与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4).
与一次函数y=x+b的图象在第一象限相交于点A(1,-k+4).
(1)试确定这两个函数的表达式;
(2)求出这两个函数图象的另一个交点B的坐标,并求△A0B的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=![]() x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,证明你的结论;
(3)点M是x轴上的一个动点,当△DCM的周长最小时,求点M的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com