
【题目】如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,则∠A=∠F,请说明理由.

解:∵∠1=∠2(已知)
∠2=∠DGF( )
∴∠1=∠DGF
∴BD∥CE( )
∴∠3+∠C=180( )
又∵∠3=∠4(已知)
∴∠4+∠C=180
∴ ∥ (同旁内角互补,两直线平行)
∴∠A=∠F( )
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
问题:如图所示,在正方形ABCD和BEFG中,点A,B,E在同一直线上,P是线段DF中点,连接PG,PC.
探究:当PG与PC的夹角为90°时,平行四边形BEFG是正方形.
小聪同学的思路是:首先可以证明四边形BEFG是矩形,然后延长GP交DC于点H,构造全等三角形,经过推理可以探索出问题答案.
请你参考小聪同学的思路,探究并解决这个问题.
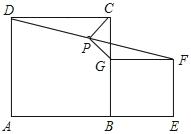
(1)求证:四边形BEFG是矩形;
(2)求证:PG与PC的夹角为90°时,四边形BEFG是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
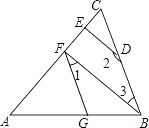
【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由地理知识可知:各地的气温受海拔高度的影响,海拔每升高100米,气温就下降0.6℃,现已知重庆的海拔高度约为260米,峨眉山的海拔高度约为3099米,则当重庆气温为28℃时,峨眉山山顶的气温为多少?(精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的两边
的两边![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,反比例函数
轴的正半轴上,反比例函数![]() (
(![]() >0)与
>0)与![]() 相交于点
相交于点![]() ,与
,与![]() 相交于点
相交于点![]() ,若
,若![]() ,且
,且![]() 的面积是5,则
的面积是5,则![]() 的值为_______.
的值为_______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com