
【题目】如图,已知直线l1∥l2,且l3与l1,l2分别交于A,B两点,l4与l1,l2相交于C,D两点,点P在直线AB上.
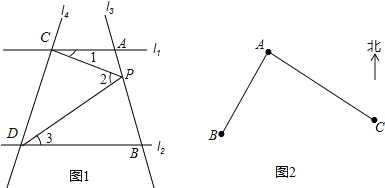
(1)【探究1】如图1,当点P在A,B两点间滑动时,试探究∠1,∠2,∠3之间的关系是否发生变化?并说明理由;
(2)【应用】如图2,A点在B处北偏东32°方向,A点在C处的北偏西56°方向,应用探究1的结论求出∠BAC的度数.
(3)【探究2】如果点P在A,B两点外侧运动时,试探究∠ACP,∠BDP,∠CPD之间的关系,并说明理由.
【答案】见解析
【解析】
试题分析:(1)过点P作PQ∥AC,交CD于点Q,由PQ∥l1∥l2结合“两直线平行,内错角相等”找出“∠1=∠CPQ,∠3=∠DPQ”,再通过角的计算即可得出结论;
(2)分别在B点和A点处画方位图,结合(1)的结论即可算出结果;
(3)分点P的位置不同来考虑:①当点P在A点上方时,过点P作PQ∥AC,交CD于点Q,由PQ∥l1∥l2结合“两直线平行,内错角相等”找出“∠QPC=∠ACP,∠QPD=∠BDP”,再通过角的计算即可得出结论;②当点P在B点下方时,过点P作PQ∥AC,交CD于点Q,利用①的方法可得出结论.综合①②即可得出结论.
解:(1)当点P在A、B两点间滑动时,∠2=∠1+∠3保持不变.理由如下:
过点P作PQ∥AC,交CD于点Q,如图1所示.

∵PQ∥AC,
∴∠1=∠CPQ,
又∵PQ∥AC,BD∥AC,
∴PQ∥BD,
∴∠3=∠DPQ,
∴∠1+∠3=∠CPQ+∠DPQ,
即∠1+∠3=∠2.
(2)分别在B点和A点处画方位图,如图2所示.

由(1)知:∠2=∠1+∠3
∴∠BAC=32°+56°=88°.
(3)①当点P在A点上方时,过点P作PQ∥AC,交CD于点Q,如图3所示.

∵PQ∥AC,
∴∠QPC=∠ACP.
又∵PQ∥AC,BD∥AC,
∴PQ∥BD,
∴∠QPD=∠BDP.
又∵∠CPD=∠QPD﹣∠QPC,
∴∠CPD=∠BDP﹣∠ACP.
②当点P在B点下方时,过点P作PQ∥AC,交CD于点Q,如图3所示.

同理可得:∠CPD=∠ACP﹣∠BDP.
综上:∠CPD=|∠ACP﹣∠BDP|.


科目:初中数学 来源: 题型:
【题目】能说明命题“关于x的一元二次方程x2+mx+4=0,当m<﹣2时必有实数解”是假命题的一个反例为( )
A. m=﹣4 B. m=﹣3 C. m=﹣2 D. m=4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在利用完全平方公式计算一个二项整式的平方时,不小心用墨水把中间一项的系数染黑了,得到正确的结果为4a2■ab+9b2,你认为这个二项整式应是( )
A. 2a+3b B. 2a﹣3b C. 2a±3b D. 4a±9b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的是( )
A.抛物线y=2x2的图象向左平移2个单位,再向下平移1个单位,则所得抛物线的解析式为y=2x2﹣8x+7
B.方程﹣x2+bx+c=0无实数根,则二次函数y=﹣x2+bx+c的图象一定在x轴下方
C.将长度为1m的木条黄金分割,较短的一段木条长为![]() m
m
D.两个等腰直角三角形一定相似
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量是第一次的2倍还多300千克,如果超市按每千克9元的价格出售,当大部分干果售出后,余下的600千克按售价的8折售完.
(1)该种干果的第一次进价是每千克多少元?
(2)超市销售这种干果共盈利多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com