
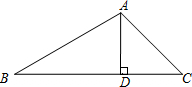
 如图,在△ABC中,∠B=30°,∠C=45°,AC=2$\sqrt{2}$.求BC边上的高及△ABC的面积.
如图,在△ABC中,∠B=30°,∠C=45°,AC=2$\sqrt{2}$.求BC边上的高及△ABC的面积. 分析 先根据AD⊥BC,∠C=45°得出△ACD是等腰直角三角形,再由AC=2$\sqrt{2}$得出AD及CD的长,由∠B=30°求出BD的长,根据三角形的面积公式即可得出结论.
解答 解:∵AD⊥BC,∠C=45°,
∴△ACD是等腰直角三角形,
∵AD=CD.
∵AC=2$\sqrt{2}$,
∴2AD2=AC2,即2AD2=8,解得AD=CD=2.
∵∠B=30°,
∴AB=2AD=4,
∴BD=$\sqrt{{AB}^{2}-{AD}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴BC=BD+CD=2$\sqrt{3}$+2,
∴S△ABC=$\frac{1}{2}$BC•AD=$\frac{1}{2}$(2$\sqrt{3}$+2)×2=2+2$\sqrt{3}$.
点评 本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
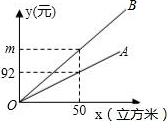 某市发改委举行居民用水价格调整听证会,届时将有两个方案提供听证.如图,射线OA、射线OB分别表示现行的、方案一的每户每月的水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;
某市发改委举行居民用水价格调整听证会,届时将有两个方案提供听证.如图,射线OA、射线OB分别表示现行的、方案一的每户每月的水费y(元)与每户每月的用水量x(立方米)之间的函数关系,已知方案一的用水价比现行的用水价每立方米多0.96元;| 阶数 | 用水量(立方米) | 用水价格(元/立方米) |
| 第一阶 | 0~15(含15)的部分 | 2.61 |
| 第二阶 | 15~25(含25)的部分 | 3.92 |
| 第三阶 | 25以上的得分 | n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
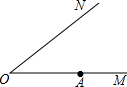 如图,已知ON是一条公路桥梁,现要在上游点A处再建一座与ON平行的大桥AB,请用尺规画出AB方向(不必写作法).并根据你的作法用一句话简单说明为什么AB和ON是平行的?
如图,已知ON是一条公路桥梁,现要在上游点A处再建一座与ON平行的大桥AB,请用尺规画出AB方向(不必写作法).并根据你的作法用一句话简单说明为什么AB和ON是平行的?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知∠AOB,画图并回答:
如图,已知∠AOB,画图并回答:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com