
【题目】如图,在△ABC中,BA=BC,D在边CB上,且DB=DA=AC.
(1)如图1,填空∠B= °,∠C= °;
(2)若M为线段BC上的点,过M作直线MH⊥AD于H,分别交直线AB、AC与点N、E,如图2
①求证:△ANE是等腰三角形;
②试写出线段BN、CE、CD之间的数量关系,并加以证明.
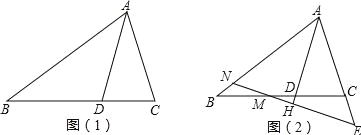
【答案】(1)36 ;72 ;(2)①证明详见解析;②CD=BN+CE,理由详见解析.
【解析】
试题分析:(1)BA=BC,且DB=DA=AC可得∠C=∠ADC=∠BAC=2∠B,∠DAC=∠B,在△ADC中由三角形内角和可求得∠B,∠C;
(2)①由(1)可知∠BAD=∠CAD=36°,且∠AHN=∠AHE=90°,可求得∠ANH=∠AEH=54°,可得AN=AE;
②由①知AN=AE,借助已知利用线段的和差可得CD=BN+CE.
试题解析:(1)∵BA=BC,
∴∠BCA=∠BAC,
∵DA=DB,
∴∠BAD=∠B,
∵AD=AC,
∴∠ADC=∠C=∠BAC=2∠B,
∴∠DAC=∠B,
∵∠DAC+∠ADC+∠C=180°,
∴2∠B+2∠B+∠B=180°,
∴∠B=36°,∠C=2∠B=72°,
故答案为:36;72;
(2)①在△ADB中,∵DB=DA,∠B=36°,
∴∠BAD=36°,
在△ACD中,∵AD=AC,
∴∠ACD=∠ADC=72°,
∴∠CAD=36°,
∴∠BAD=∠CAD=36°,
∵MH⊥AD,
∴∠AHN=∠AHE=90°,
∴∠AEN=∠ANE=54°,
∴AN=AE,
即△ANE是等腰三角形;
②CD=BN+CE.
证明:由①知AN=AE,
又∵BA=BC,DB=AC,
∴BN=AB﹣AN=BC﹣AE,CE=AE﹣AC=AE﹣BD,
∴BN+CE=BC﹣BD=CD,
即CD=BN+CE.


科目:初中数学 来源: 题型:
【题目】完成下面推理过程:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:

∵∠1=∠2(已知),
且∠1=∠CGD( ),
∴∠2=∠CGD(等量代换).
∴CE∥BF( ).
∴∠ =∠C( ).
又∵∠B=∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠MON=40°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O重合),连接AC交射线OE于点D.设∠OAC= ![]() °.
°.
(1)如图1,若AB//ON,则①∠ABO的度数是______;②当∠BAD=∠ABD时, ![]() =______;③当∠BAD=∠BDA时,
=______;③当∠BAD=∠BDA时, ![]() =______.
=______.
(2)如图2,若AB⊥OM,则是否存在这样的x的值,使得△ADB中有两个相等的角?若存在,求出x的值;若不存在,说明理由.
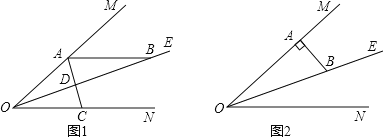
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,则下列结论:
①AD⊥BD;②∠AOC=∠AEC;③CB平分∠ABD;④AF=DF;⑤BD=2OF;⑥△CEF≌△BED,其中一定成立的是( )
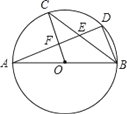
A. ②④⑤⑥ B. ①③⑤⑥ C. ②③④⑥ D. ①③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
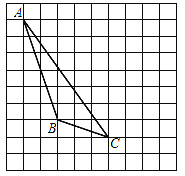
【题目】如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
(1)画出△A′B′C′;
(2)利用网格点和直尺画图:画出AB边上的高线CD;
(3)图中△ABC的面积是 ;
(4)△ABC与△EBC面积相等,点E是异于A点的格点,则这样的E点有 个.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com