练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】只有1和它本身两个因数且大于1的正整数叫做素数．我国数学家陈景润哥德巴赫猜想的研究中取得了世界领先的成果．哥德巴赫猜想是“每个大于2的偶数都表示为两个素数的和”，如10=3+7．

    （1）从7，11，13，17这4个素数中随机抽取一个，则抽到的数是11的概率是_____；

    （2）从7，11，13，17这4个素数中随机抽取1个数，再从余下的3个数中随机抽取1个数，用画树状图或列表的方法，求抽到的两个素数之和等于24的概率．

    【答案】（1）；（2）．

    【解析】

    （1）)四个数中，抽到11只有一种可能，根据概率公式直接计算即可得；

    （2）画树状图得到所有等可能的情况，然后再从中找出符合条件的结果数，利用概率公式进行计算即可.

    解：（1）在7，11，13，17中，抽到11的概率是；

    （2）列表如下：

    7

    11

    13

    17

    7

    *

    18

    20

    24

    11

    18

    *

    24

    28

    13

    20

    24

    *

    30

    17

    24

    28

    30

    *

    由表可以看出，分别从这4个素数中随机抽取1个数，再从余下的3个数中随机抽取1个数，可能出现的结果有12种，并且他们出现的可能性相等，抽到的两个素数之和等于24的有4种情况．

    所以，抽到的两个素数之和等于24的概率为P=．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】“推进全科阅读，培育时代新人”．某学校为了更好地开展学生读书活动，随机调查了九年级50名学生最近一周的读书时间，统计数据如下表：

    时间（小时）

    6

    7

    8

    9

    10

    人数

    5

    8

    12

    15

    10

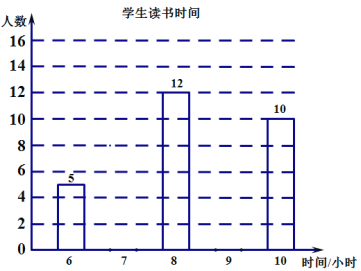
    （1）根据上述表格补全下面的条形统计图；

    （2）写出这50名学生读书时间的众数、中位数、平均数；

    （3）若该校有1000名学生，求最近一周的读书时间不少于7小时的人数？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

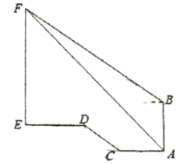
    【题目】学校某数学兴趣小组想测学校旗杆高度如图，明明在稻香园一楼点测得旗杆顶点仰角为，在稻香园二楼点测得点的仰角为．明明从点朝旗杆方向步行米到点，沿坡度的台阶走到点，再向前走米到旗杆底部，已知稻香园高度为米，则旗杆的高度约为（ ）（参考数据：，，）

    A.米B.米C.米D.米

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC与△ABD中，∠DBA＝∠CAB，AC与BD交于点F

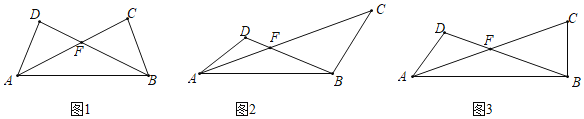
    （1）如图1，若∠DAF＝∠CBF，求证：AD＝BC；

    （2）如图2，∠D＝135°，∠C＝45°，AD＝2，AC＝4，求BD的长．

    （3）如图3，若∠DBA＝18°，∠D＝108°，∠C＝72°，AD＝1，直接写出DB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知一次函数的图像与反比例函数的图像交于点，与轴交于点，若，且．

    （1）求反比例函数与一次函数的表达式；

    （2）若点为轴上一点，是等腰三角形，求点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线经过点A(-3，0)，C(0，3)，交x轴于另一点B，其顶点为D．

    （1）求抛物线的解析式；

    （2）点P为抛物线上一点，直线CP交x轴于点E，若△CAE与△OCD相似，求P点坐标；

    （3）如果点F在y轴上，点M在直线AC上，那么在抛物线上是否存在点N，使得以C，F，M，N为顶点的四边形是菱形？若存在，请求出菱形的周长；若不存在，请说明理由．

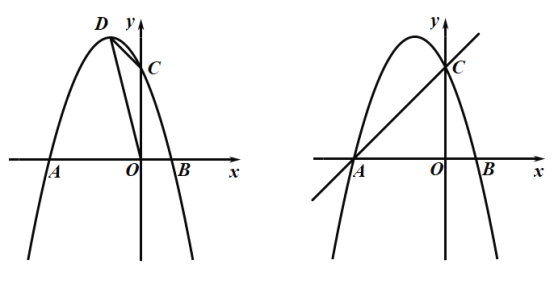
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，小明在大楼30米高（即PH＝30米）的窗口P处进行观测，测得山坡上A处的俯角∠APQ为15°，山脚B处的俯角∠BPQ为60°，已知该山坡的坡度i（即tan∠ABC）为1：，点P，H，B，C，A在同一个平面上，点H、B、C在同一条直线上，且PH丄HC．

    （1）求出山坡坡角（∠ABC）的大小；

    （2）求A、B两点间的距离（结果精确到0.1米，参考数据：≈1.732）．

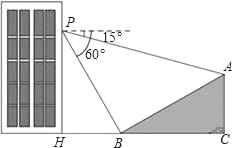
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y＝﹣x2+bx+c经过点A（4，3），顶点为B，对称轴是直线x＝2．

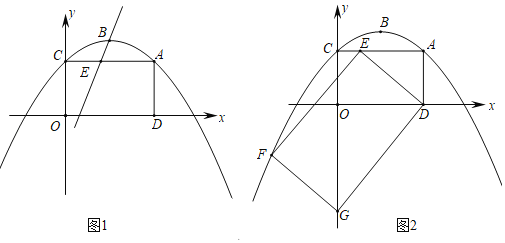
    （1）求抛物线的函数表达式和顶点B的坐标；

    （2）如图1，抛物线与y轴交于点C，连接AC，过A作AD⊥x轴于点D，E是线段AC上的动点（点E不与A，C两点重合）；

    （i）若直线BE将四边形ACOD分成面积比为1：3的两部分，求点E的坐标；

    （ii）如图2，连接DE，作矩形DEFG，在点E的运动过程中，是否存在点G落在y轴上的同时点F恰好落在抛物线上？若存在，求出此时AE的长；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，直线与x轴，y轴分别交于点A，B，点在第一象限内，连结，，．动点P在上从点A向终点B匀速运动，同时，动点Q在上从点C向终点O匀速运动，它们同时到达终点，连结交于点D．

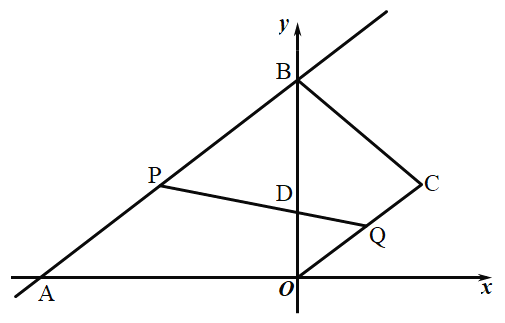
    （1）求点B的坐标和a的值；

    （2）当点Q运动到中点时，连结，求的面积；

    （3）作交直线于点R．

    ①当为等腰三角形时，求的长度；

    ②记交于点E，连结，则的最小值为__________．（直接写出答案）

    查看答案和解析>>

    同步练习册答案