
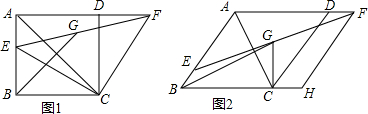
���� ��1�����ı���ABCD�������Σ��õ�BC=CD����ABC=��ADC=90�㣬����ȫ�������ε����ʵõ�CE=CF���Ƴ���ECF�ǵ���ֱ�������Σ����ݵ���ֱ�������ε����ʼ��ɵõ����ۣ�
��2������AG��CG�����ݵ���ֱ�������ε����ʵõ�CG=$\frac{1}{2}$EF��֤��AG=CG������ȫ�������ε����ʵõ���ABG=��CBG�����ɵõ����ۣ�
��3���ӳ�AG��FH��M������CM������ƽ���ߵ����ʵõ���AEG=��GFM������ȫ�������ε����ʵõ�AG=GM��MF=AE������ƽ���ı��ε����ʵõ�AB=HF��ͨ����BAG�ա�BCG���õ���ABG=��CBG�����ɵõ����ۣ�
��� 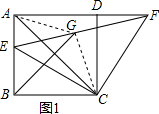 �⣺��1�����ı���ABCD�������Σ�
�⣺��1�����ı���ABCD�������Σ�
��BC=CD����ABC=��ADC=90�㣬
���CDF=90�㣬
�ڡ�CBF���CDF�У�$\left\{\begin{array}{l}{CB=CD}\\{��CBE=��CDF}\\{BE=DF}\end{array}\right.$��
��CE=CF��
���BCE=��DCF��
���BCE+��ECD=��DCF+ECD��
���BCD=��ECF=90�㣬
���ECF�ǵ���ֱ�������Σ�
��EF=$\sqrt{2}$CE=2$\sqrt{2}$��
��2����ͼ1������AG��CG��
�ߡ�ECF�ǵ���ֱ�������Σ�G��EF���е㣬
��CG=$\frac{1}{2}$EF��
��AG=$\frac{1}{2}$EF��
��AG=CG��
�ڡ�BAG���BCG�У�$\left\{\begin{array}{l}{BA=BC}\\{AG=CG}\\{BG=BG}\end{array}\right.$��
���BAG�ա�BCG����ABG=��CBG��
��BA=BC��
��BG��AC��OA=OC��
��BG��ֱƽ��AC��
��3�����������ɣ���ͼ2���ӳ�AG��FH��M������CM��
��AE��FH��
���AEG=��GFM��
�ڡ�AEG���MFG�У�$\left\{\begin{array}{l}{��AEG=��GFM}\\{EG=FG}\\{��AGE=��MGF}\end{array}\right.$��
���AGE�ա�MFG��
��AG=GM��MF=AE��
��FH��AB��AF��AE��
���ı���ABHF��ƽ���ı��Σ�
��AB=HF��
��BE=HM��
��BE=DF=CH��
��CH=HM��
���MCH=��BCA����ABC+��H=180�㣬
���BAC+��BCA+��MCH+��HMC=180�㣬
��2��BCA+2��HCM=180�㣬
���BCA+��HCM=90�㣬
���ACM=90�㣬
��Rt��ACM��AG=GM��
��CG=$\frac{1}{2}$AM=AG��
��Rt��BAG��Rt��BCG��$\left\{\begin{array}{l}{AB=BC}\\{AG=CG}\\{BG=BG}\end{array}\right.$��
���BAG�ա�BCG��
���ABG=��CBG��
��BA=BC��
��BG��AC��AO=CO��
��BG��ֱƽ��AC��
���� ���⿼���������ε����ʣ�ƽ���ı��ε��ж������ʣ�����ֱ�������ε����ʣ�ȫ�������ε��ж������ʣ��߶δ�ֱƽ���ߵ��ж������ʣ���ȷ�����������߹���ȫ���������ǽ���Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC�У�AB=AC��E��F�ֱ���BC��AC���е㣬��ACΪб����Rt��ADC��
��ͼ����ABC�У�AB=AC��E��F�ֱ���BC��AC���е㣬��ACΪб����Rt��ADC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ������һλ���ĵ�ͬѧ�������Լ����꼶��һѧ�ڵ���ѧ�������ɼ�����λ���֣�����ͳ�ƣ��������
������һλ���ĵ�ͬѧ�������Լ����꼶��һѧ�ڵ���ѧ�������ɼ�����λ���֣�����ͳ�ƣ��������| ����������� | ƽʱ | ���� | ��ĩ | |||
| ���1 | ���2 | ���3 | ���4 | |||
| �ɼ� | 90 | 76 | 85 | 89 | 87 | 92 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڵ�����ABC�У�AB=AC����O�ǡ�ABC��һ�㣬��OB=OC������AO���ӳ�����BC�ڵ�D�����BD=6����ôBC��ֵΪ12��
��ͼ���ڵ�����ABC�У�AB=AC����O�ǡ�ABC��һ�㣬��OB=OC������AO���ӳ�����BC�ڵ�D�����BD=6����ôBC��ֵΪ12���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
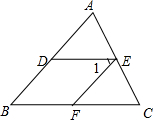 ��ͼ����AED=��C����1=��B��˵����EF��AB
��ͼ����AED=��C����1=��B��˵����EF��AB�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ������/�� | ����ֵ | Ƶ���������� | Ƶ�� |
| 60��x��70 | 65 | 30 | 0.15 |
| 70��x��80 | 75 | b | 0.45 |
| 80��x��90 | 85 | 60 | c |
| 90��x��100 | a | 20 | 0.1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | m��1 | B�� | m��0 | C�� | m��0 | D�� | m��1 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com