
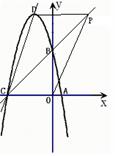
(本小题10分)如图, 抛物线![]() 与x轴的一个交点是A,与y轴的交点是B,且OA、OB(OA<OB)的长是方程
与x轴的一个交点是A,与y轴的交点是B,且OA、OB(OA<OB)的长是方程![]() 的两个实数根.
的两个实数根.

1.(1)求A、B两点的坐标;
2. (2) 求出此抛物线的的解析式及顶点D的坐标;
3.(3)求出此抛物线与x轴的另一个交点C的坐标;
4.(4)在直线BC上是否存在一点P,使四边形PDCO为梯形?若存在,求出P点坐标,若不存在,说明理由.
1.解:(1)∵![]() 的两个实数根为
的两个实数根为![]()
OA、OB(OA<OB)的长是方程![]() 的两个实数根
的两个实数根
∴ OA=1,OB=5
∴A(1,0), B(0,5)
2.(2)∵抛物线![]() 与x轴的一个交点是A,与y轴的交点是B
与x轴的一个交点是A,与y轴的交点是B
∴![]()
解得:![]()
∴所求二次函数的解析式为:![]() -------------------------3分
-------------------------3分
顶点坐标为:D(-2,9)
3.(3)此抛物线与x轴的另一个交点C的坐标为(-5,0)
4.(4)直线CD的解析式为:
y=3x+15 --------------------------6分
直线BC的解析式为:
y=x+5 ---------------------------7分
①若以CD为底,则OP∥CD
直线OP的解析式为:y=3x
 于是有
于是有![]() 解得:
解得: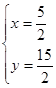
∴点P的坐标为(![]() --------------8分
--------------8分
②若以OC为底,则DP∥CO
直线DP的解析式为:y=9
于是有![]() 解得:
解得:![]()
∴点P的坐标为(4,9) --------------------------9分
∴在直线BC上存在点P,使四边形PDCO为梯形且P点坐标为(![]() 或
或
(4,9)
解析:略


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2011-2012学年江苏省启东市九年级寒假作业检测数学卷 题型:解答题
(本小题10分)
如图,抛物线 与x轴交与A(1,0),B(- 3,0)两点,
与x轴交与A(1,0),B(- 3,0)两点,
1.(1)求该抛物线的解析式;
2.(2)抛物线交y轴与C点,在该抛物线的对称轴上是否存在点Q,使得△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2012届北京一六三中初三上学期模拟数学卷 题型:解答题
(本小题10分)如图, 抛物线 与x轴的一个交点是A,与y轴的交点是B,且OA、OB(OA<OB)的长是方程
与x轴的一个交点是A,与y轴的交点是B,且OA、OB(OA<OB)的长是方程 的两个实数根.
的两个实数根.

1.(1)求A、B两点的坐标;
2. (2) 求出此抛物线的的解析式及顶点D的坐标;
3.(3)求出此抛物线与x轴的另一个交点C的坐标;
4.(4)在直线BC上是否存在一点P,使四边形PDCO为梯形?若存在,求出P点坐标,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(四川内江卷)数学 题型:解答题
(本小题10分)如图11,已知二次函数y= -x2 +mx +4m的图象与x轴交于
A(x1,0),B(x2,0)两点(B点在A点的右边),与y轴的正半轴交于点C,且(x1+x2) - x1x2=10.
(1)求此二次函数的解析式.
(2)写出B,C两点的坐标及抛物线顶点M的坐标;
(3)连结BM,动点P在线段BM上运动(不含端点B,M),过点P作x轴的垂线,垂足为H,设OH的长度为t,四边形PCOH的面积为S.请探究:四边形PCOH的面积S有无最大值?如果有,请求出这个最大值;如果没有,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com