
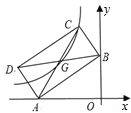
【题目】如图,矩形ABCD的两个顶点A、B分别在x、y轴上,顶点C、D位于第二象限,且OA=3,OB=2,对角线AC、BD交于点G,若双曲线![]() 经过C、G,则k=__________.
经过C、G,则k=__________.
【答案】-3.5
【解析】
分别过C、G两点作x轴的垂线,交x轴于点E、F,作CH⊥y轴于H,设![]() ,根据矩形的性质与平行线分线段成比例得出点G的坐标,根据反比例函数系数k=xy求出点m,通过证明△AOB∽△BHC,求得CE,得出点C坐标,进而求解.
,根据矩形的性质与平行线分线段成比例得出点G的坐标,根据反比例函数系数k=xy求出点m,通过证明△AOB∽△BHC,求得CE,得出点C坐标,进而求解.
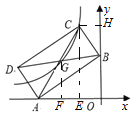
如图,分别过C、G两点作x轴的垂线,交x轴于点E、F,作CH⊥y轴于H,
∴CE∥GF,设![]() ,
,
∵四边形ABCD是矩形,
∴AG=CG,
∴GF=![]() CE,EF=
CE,EF=![]() ,
,
∴OF=![]() ,
,
∴![]() ,
,
∵曲线![]() 经过点C、G,
经过点C、G,
∴![]() ,
,
解得,![]() ,
,
∴CH=1,
∵∠ABC=90°,
∴∠CBH+∠ABO=90°,
∵∠OAB+∠ABO=90°,
∴∠OAB=∠CBH,
∵∠AOB=∠BHC=90°,
∴△AOB∽△BHC,
∴![]() ,即
,即![]() ,
,
∴BH=![]() ,
,
∴OH=![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案为:-3.5.


科目:初中数学 来源: 题型:
【题目】如图,将直角三角板![]() 的直角边
的直角边![]() 放在半圆
放在半圆![]() 的直径
的直径![]() 上,直角顶点
上,直角顶点![]() 与直径端点
与直径端点![]() 重合,已知
重合,已知![]() ,且
,且![]() 的直角边
的直角边![]() 与半圆
与半圆![]() 的半径
的半径![]() 长均为2.现将直角三角板
长均为2.现将直角三角板![]() 沿直径
沿直径![]() 的方向向右平移,将三角板
的方向向右平移,将三角板![]() 平移后的三角形记为
平移后的三角形记为![]() .
.
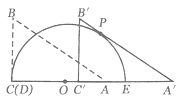
(1)如图,当![]() 平移到斜边与半圆相切时,试求
平移到斜边与半圆相切时,试求![]() 的长度(结果保留
的长度(结果保留![]() );
);
(2)设平移距离为![]() ,在直角三角形
,在直角三角形![]() 平移过程中,折线
平移过程中,折线![]() (包括端点)与半圆弧共有3个交点时,求
(包括端点)与半圆弧共有3个交点时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2,其中正确的结论分别是___.
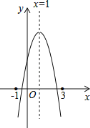
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=(-a2+a)x2+x+1(a≠0)
(1)无论a为何值,抛物线C总是经过一个定点,该定点的坐标为_____.
(2)无论a为何值,该抛物线的顶点总在一条固定的直线上运动,求出该直线的解析式.
(3)当0<y≤2时,y>0恒成立,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
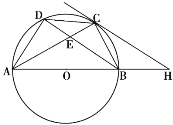
【题目】如图,点A,B,C,D是直径为AB的⊙O上四个点,C是劣弧![]() 的中点,AC交BD于点E,AE=2,EC=1.
的中点,AC交BD于点E,AE=2,EC=1.
(1)求证:△DEC∽△ADC;
(2)连结DO,探究四边形OBCD是否是菱形?若是,请你给予证明;若不是,请说明理由;
(3)延长AB到H,使BH=OB,求证:CH是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新型冠状病毒肺炎疫情发生后,全社会积极参与疫情防控工作,某市为了尽快完成100万只口罩的生产任务,安排甲、乙两个大型工厂完成.已知甲厂每天能生产口罩的数量是乙厂每天能生产口罩的数量的1.5倍,并且在独立完成60万只口罩的生产任务时,甲厂比乙厂少用5天.问至少应安排两个工厂工作多少天才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
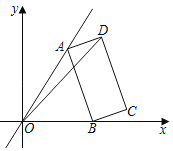
【题目】如图,在平面直角坐标系中,点A在一次函数y=![]() x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2
x位于第一象限的图象上运动,点B在x轴正半轴上运动,在AB右侧以它为边作矩形ABCD,且AB=2![]() ,AD=1,则OD的最大值是( )
,AD=1,则OD的最大值是( )
A.![]() B.
B.![]() +2C.
+2C.![]() +2D.
+2D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《算法统宗》是一本通俗实用的数学书,也是将数字入诗的代表作,这本书由明代程大位花了近20年完成,他原本是一位商人,经商之便搜集各地算书和文字方面的书籍,编成首首的歌谣口诀,将枯燥的数学问题化成美妙的诗歌,读来朗朗上口,程大位还有一首类似二元一次方程组的饮酒数学诗:“肆中饮客乱纷纷,薄酒名脑厚酒醇.醇酒一瓶醉三客,薄酒三瓶醉一人,共同饮了一十九,三十三客醉颜生,试问高明能算士,几多酵酒几多醇?”这首诗是说,好酒一瓶,可以醉倒3位客人;薄酒三瓶,可以醉倒一位客人,如果33位客人醉倒了,他们总共饮下19瓶酒.试问:其中好酒、薄酒分别是多少瓶?设有好酒x瓶,薄酒y瓶.根据题意,可列方程组为( )
A. ![]() B.
B.  C.
C. 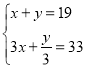 D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com