
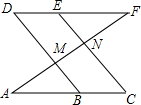
 如图.已知∠D=∠C,∠AMB=∠ENF,求证:DF∥AC.
如图.已知∠D=∠C,∠AMB=∠ENF,求证:DF∥AC. 科目:初中数学 来源: 题型:解答题
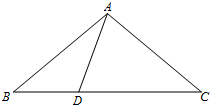 在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.
在△ABC中,已知D为直线BC上一点,若∠ABC=x°,∠BAD=y°.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,某数学学习兴趣小组为了测量树AB的度数,他们测得此树在阳光下的影子BC的长为9m,在相同时刻,他们还测得小亮在阳光下的影长为1.5m,已知小亮的身高为1.8m,则树AB的高为( )
如图,某数学学习兴趣小组为了测量树AB的度数,他们测得此树在阳光下的影子BC的长为9m,在相同时刻,他们还测得小亮在阳光下的影长为1.5m,已知小亮的身高为1.8m,则树AB的高为( )| A. | 10.8m | B. | 9m | C. | 7.5m | D. | 0.3m |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知三角形ABC的三个顶点A、B、C的坐标分别是(0,2)、(-3,0)、(1,-2),在下图的平面直角坐标系中表示出来,并根据图形回答下列问题.
已知三角形ABC的三个顶点A、B、C的坐标分别是(0,2)、(-3,0)、(1,-2),在下图的平面直角坐标系中表示出来,并根据图形回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,河堤横断面堤高BC=$5\sqrt{3}$米,迎水坡面AB的坡度为$\frac{{\sqrt{3}}}{3}$(坡度是指坡面的铅直高度与水平宽度之比,又称坡比),则AC的长是( )
如图所示,河堤横断面堤高BC=$5\sqrt{3}$米,迎水坡面AB的坡度为$\frac{{\sqrt{3}}}{3}$(坡度是指坡面的铅直高度与水平宽度之比,又称坡比),则AC的长是( )| A. | $5\sqrt{3}$米 | B. | 10米 | C. | 15米 | D. | 10$\sqrt{3}$米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D,BE平分AC,则DE=$\frac{\sqrt{5}-2}{2}$.
如图,在△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D,BE平分AC,则DE=$\frac{\sqrt{5}-2}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且∠BDA=90°,猜想线段BF、FC的数量关系,并说明理由.
如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且∠BDA=90°,猜想线段BF、FC的数量关系,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com