
分析 (1)设租用一辆甲种客车的费用为x元,则一辆乙种客车的费用为(x+100)元,列出方程即可解决问题;
(2)由题意w=300x+400(7-x)=-100x+2800,列出不等式求出x的取值范围,利用一次函数的性质即可解决问题.
解答 解:(1)设租用一辆甲种客车的费用为x元,则一辆乙种客车的费用为(x+100)元,
由题意5x+2(x+100)=2300,
解得x=300,
答:租用一辆甲种客车的费用为300元,则一辆乙种客车的费用为400元.
(2)由题意w=300x+400(7-x)=-100x+2800,
又30x+45(7-x)≥275,
解得x≤$\frac{8}{3}$,
∴x的最大值为2,
∵-100<0,
∴x=2时,w的值最小,最小值为2600.
答:当租用甲种客车2辆时,总租车费最少,最少费用为2600元.
点评 本题考查一元一次方程的应用、一次函数的应用、一元一次不等式的应用等知识,解题的关键是理解题意,学会构建一次函数解决最值问题.


科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{0.1}$ | B. | $\sqrt{8}$ | C. | $\sqrt{{x^2}+{x^2}y}$ | D. | $\sqrt{{x^2}+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
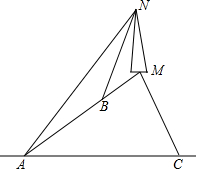 如图所示,在小山顶上有一座信号发射塔MN,在山坡坡脚A处测得塔尖点N的仰角为45°,某人沿坡度为i=1:$\sqrt{3}$坡面上山,行走200米到B处,测得塔尖点N的仰角为60°,已知A,B,M在同一条直线上,求:
如图所示,在小山顶上有一座信号发射塔MN,在山坡坡脚A处测得塔尖点N的仰角为45°,某人沿坡度为i=1:$\sqrt{3}$坡面上山,行走200米到B处,测得塔尖点N的仰角为60°,已知A,B,M在同一条直线上,求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 1或$\frac{9}{4}$ | D. | -1或-$\frac{9}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com