
【题目】点O在直线PQ上,过点O作射线OC,使∠POC=130°,将一直角三角板的直角顶点放在点O处.
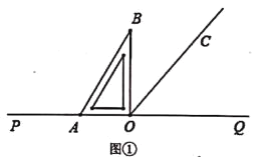
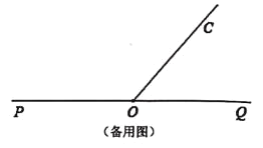
(1)如图①所示,将直角三角板AOB的一边OA与射线OP重合,则∠BOC=________°.
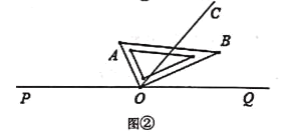
(2)将图①中的直角三角板AOB绕点O旋转一定角度得到如图②所示的位置,若OA平分∠POC,求∠BOQ的度数.
(3)将图①中的直角三角板AOB绕点O旋转一周,存在某一时刻恰有OB⊥OC,求出所有满足条件的∠AOQ的度数.
【答案】(1)40;(2)25°;(3)130°或50°
【解析】
(1))根据∠BOC=∠POC90°代入数据计算即可;
(2)2)根据角平分线的定义可得∠AOP=∠AOC= ![]() ∠POC=
∠POC= ![]() ×130°=65°,再由∠BOQ=180°-∠OP-∠AOB计算即可;
×130°=65°,再由∠BOQ=180°-∠OP-∠AOB计算即可;
(3)分当OB在∠POC内部时和当OB在∠POC外部时,计算即可.
解:(1)∵∠BOC=∠POC-∠AOB
∴∠BOC=130°-90°=40°.
故答案为:40°.
(2)解:∵OA平分∠POC,
∴∠AOP=∠AOC= ![]() ∠POC=
∠POC= ![]() ×130°=65°
×130°=65°
∴∠BOQ=180°-∠OP-∠AOB=180-65°-90°=25°
(3)解:如图1,当OB在∠POC内部时,则∠AOC=180°,
∴∠AOQ=∠POC=130
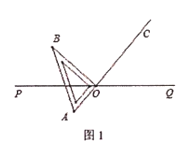
如图2,当OB在∠POC外部时,则OA与OC重合,

∴∠AOQ=∠COQ=180°-130°=50°
综上所述,∠AOQ的度数为130°或50°


 智能训练练测考系列答案
智能训练练测考系列答案科目:初中数学 来源: 题型:
【题目】一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:
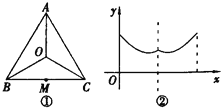
A. A→O→B B. B→A→C C. B→O→C D. C→B→O
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD,AB=4,BC=12,E、F分别是AD、BC边上的点,ED=3.将矩形纸片沿EF折叠,使点C落在AD边上的点G处,点D落在点H处.
(1)矩形纸片ABCD的面积为
(2)如图1,连结EC,四边形CEGF是什么特殊四边形,为什么?
(3)M,N是AB边上的两个动点,且不与点A,B重合,MN=1,求四边形EFMN周长的最小值.(计算结果保留根号)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与y轴交于点A,与x轴交于点B,点A的纵坐标、点B的横坐标如图所示.
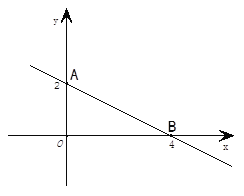
(1)求直线AB的解析式;
(2)点P在直线AB上,是否存在点P使得△AOP的面积为1,如果有请直接写出所有满足条件的点P的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
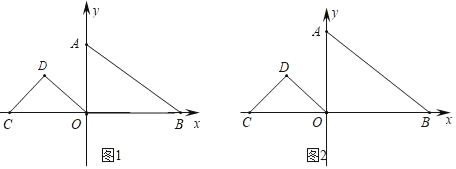
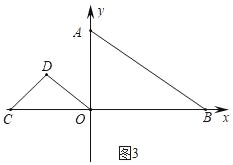
【题目】如图,已知在平面直角坐标系中,直线AB:![]() 与x轴、y轴分别交于B、A两点,等腰Rt△OCD,∠D=90°,C坐标为(﹣4,0).
与x轴、y轴分别交于B、A两点,等腰Rt△OCD,∠D=90°,C坐标为(﹣4,0).
(1)求A、B坐标;
(2)将△OCD沿x轴正方形平移,速度为1个单位为每秒,时间为t(0≤t≤6),设△OCD与△OAB重叠面积为S,请写出S与t之间的函数关系式;
(3)将△OCD绕O点旋转,当O、B、D三点构成的三角形为直角三角形时,请直接写出D点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从左至右第1个图由1个正六边形,6个正方形和6个等边三角形组成;第二个图由2个正六边形、11个正方形和10个等边三角形组成;第3个图由3个正六边形、16个正方形和14个等边三角形组成按此规律,第![]() 个图中正方形和等边三角形的个数之和为( )
个图中正方形和等边三角形的个数之和为( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
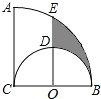
【题目】如图,![]() ,
,![]() ,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作
,以BC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作![]() ,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是
,过点O作AC的平行线交两弧于点D、E,则阴影部分的面积是![]()
![]()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
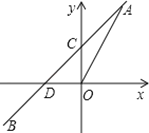
【题目】如图,正比例函数y=2x的图象与一次函数y=kx+b的图象交于点A(m,2),一次函数图象经过点B(-2,1),与y轴的交点为C,与x轴的交点为D.
(1)求一次函数解析式;
(2)求△AOD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
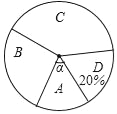
【题目】我市某中学举行演讲比赛,赛后整理参赛学生的成绩,将比赛成绩分为A,B,C,D四个等级,把结果列成下表(其中,m是常数)并绘制如图所示的扇形统计图(部分).
等级 | A | B | C | D |
人数 | 6 | 10 | m | 8 |
(1)求m的值和A等级所占圆心角α的大小;
(2)若从本次比赛中获得A等级的学生中,选出2名取参加市中心学生演讲比赛,已知A等级中男生有2名,求出所选2名学生中恰好是一名男生和一名女生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com