
我们知道,三角形的三条中线一定会交于一点,这一点就叫做三角形的重心。重心有很多美妙的性质,如在关线段比.面积比就有一些“漂亮”结论,利用这些性质可以解决三角形中的若干问题。请你利用重心的概念完成如下问题:
(1)若O是△ABC的重心(如图1),连结AO并延长交BC于D,证明:![]() ;
;
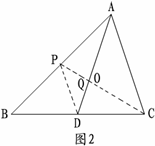
(2)若AD是△ABC的一条中线(如图2),O是AD上一点,且满足![]() ,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
(3)若O是△ABC的重心,过O的一条直线分别与AB、AC相交于G、H(均不与△ABC的顶点重合)(如图3),S四边形BCHG.S△AGH分别表示四边形BCHG和△AGH的面积,试探究![]() 的最大值。
的最大值。

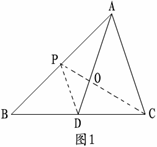 解:(1)证明:如图1,连结CO并延长交AB于点P,连结PD。
解:(1)证明:如图1,连结CO并延长交AB于点P,连结PD。
∵点O是△ABC的重心,
∴P是AB的中点,D是BC的中点,PD是△ABC的中位线,AC=2PD, AC // PD,
∠DPO=∠ACO,∠PDO=∠CAO,
 △OPD∽△CA,
△OPD∽△CA,![]() =
= ![]() =
= ![]() ,
, ![]() =
= ![]()
![]() ,∴
,∴![]() ;
;
(2)点O是是△ABC的重心。
证明:如图2,作△ABC的中线CP,与 AB边交于点P,与△ABC的另一条中线AD交于点Q,则点Q是△ABC的重心,根据(1)中的证明可知 ![]() ,
,
而 ![]() ,点Q与点O重合(是同一个点),所以点O是△ABC的重心;
,点Q与点O重合(是同一个点),所以点O是△ABC的重心;
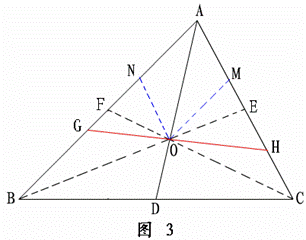 (3)如图3,连结CO交AB于F,连结BO交AC于E,过点O分别作AB、AC的平行线OM、ON,分别
(3)如图3,连结CO交AB于F,连结BO交AC于E,过点O分别作AB、AC的平行线OM、ON,分别
与AC、AB交于点M、N,
∵点O是△ABC的重心,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∵ 在△ABE中,OM//AB,![]() =
= ![]() =
= ![]() ,OM =
,OM = ![]() AB,
AB,
在△ACF中,ON//AC,![]() =
= ![]() =
= ![]() ,ON =
,ON = ![]() AC,
AC,
在△AGH中,OM//AH,![]() =
= ![]() ,
,
在△ACH中,ON//AH,![]() =
= ![]() ,
,
∴ ![]() +
+ ![]() =
= ![]() +
+![]() =1,
=1, ![]() +
+ ![]() =1,
=1, ![]() +
+ ![]() = 3 ,
= 3 ,
令![]() = m ,
= m , ![]() = n , m=3-n,
= n , m=3-n,
∵![]() =
= ![]() ,
,
![]() =
= 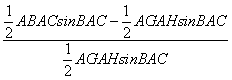 =
=![]()
= ![]() -1= mn-1=(3-n)n-1= -n2 +3n-1= -(n-
-1= mn-1=(3-n)n-1= -n2 +3n-1= -(n- ![]() )2 +
)2 + ![]() ,
,
∴ 当 ![]() = n =
= n = ![]() ,GH//BC时,
,GH//BC时,![]() 有最大值
有最大值 ![]() 。
。
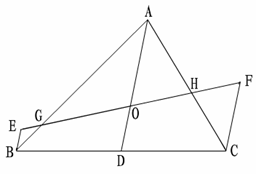
附:![]() 或
或 ![]() 的另外两种证明方法的作图。
的另外两种证明方法的作图。
方法一:分别过点B、C作AD的平行线BE、CF,分别交直线GH于点E、F。
方法二:分别过点B、C、A、D作直线GH的垂线,垂足分别为E、F、N、M。
 下面的图解也能说明问题:
下面的图解也能说明问题:



 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:初中数学 来源: 题型:
| AO |
| AD |
| 2 |
| 3 |
| AO |
| AD |
| 2 |
| 3 |
| S四边形BCHG |
| S△AGH |

查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(四川绵阳卷)数学(解析版) 题型:解答题
(2013年四川绵阳14分)我们知道,三角形的三条中线一定会交于一点,这一点就叫做三角形的重心.重心有很多美妙的性质,如关于线段比.面积比就有一些“漂亮”结论,利用这些性质可以解决三角形中的若干问题.请你利用重心的概念完成如下问题:

(1)若O是△ABC的重心(如图1),连结AO并延长交BC于D,证明: ;
;
(2)若AD是△ABC的一条中线(如图2),O是AD上一点,且满足 ,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
(3)若O是△ABC的重心,过O的一条直线分别与AB、AC相交于G、H(均不与△ABC的顶点重合)(如图3),S四边形BCHG,S△AGH分别表示四边形BCHG和△AGH的面积,试探究 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
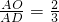 ;
;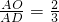 ,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;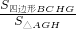 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源:2013年四川省绵阳市中考数学试卷(解析版) 题型:解答题
 ;
; ,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由;
,试判断O是△ABC的重心吗?如果是,请证明;如果不是,请说明理由; 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com