
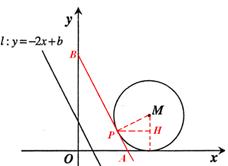
 :y=-2x+b (b≥0)的位置随b的不同取值而变化.
:y=-2x+b (b≥0)的位置随b的不同取值而变化. :y=-2x+b (b≥0)经过圆心M:
:y=-2x+b (b≥0)经过圆心M: :y=-2x+b(b≥0)与OM相切:
:y=-2x+b(b≥0)与OM相切: 扫过矩形ABCD的面积为S,当b由小到大变化时,请求出S与b的函数关系式,
扫过矩形ABCD的面积为S,当b由小到大变化时,请求出S与b的函数关系式,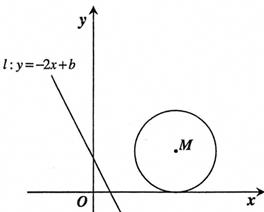

 。
。 经过A(2,0)时,b=4;当直线
经过A(2,0)时,b=4;当直线 经过D(2,2)时,b=6;当直线
经过D(2,2)时,b=6;当直线 经过B(6,0)时,b=12;当直线
经过B(6,0)时,b=12;当直线 经过C(6,2)时,b=14。
经过C(6,2)时,b=14。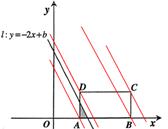
 扫过矩形ABCD的面积S为0。
扫过矩形ABCD的面积S为0。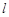 扫过矩形ABCD的面积S为△EFA的面积(如图1),
扫过矩形ABCD的面积S为△EFA的面积(如图1),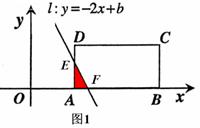
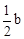 ,则F(
,则F(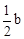 ,0)。
,0)。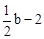 ,AE=-4+b。
,AE=-4+b。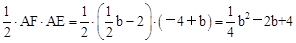 。
。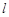 扫过矩形ABCD的面积S为直角梯形DHGA的面积(如图2),
扫过矩形ABCD的面积S为直角梯形DHGA的面积(如图2),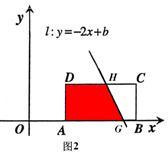
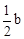 ,则G(
,则G(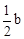 ,0),
,0),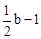 ,则H(
,则H(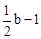 ,2)。
,2)。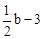 ,AG=
,AG=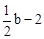 。AD=2
。AD=2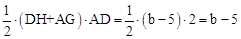 。
。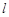 扫过矩形ABCD的面积S为五边形DMNBA的面积=矩形ABCD的面积-△CMN的面积(如图3)
扫过矩形ABCD的面积S为五边形DMNBA的面积=矩形ABCD的面积-△CMN的面积(如图3)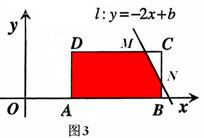
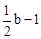 ,则M(
,则M(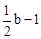 ,0),
,0),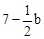 ,NC=14-b。
,NC=14-b。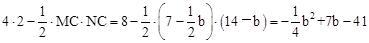 。
。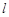 扫过矩形ABCD的面积S为矩形ABCD的面积,面积为民8。
扫过矩形ABCD的面积S为矩形ABCD的面积,面积为民8。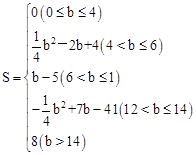 。
。
 。
。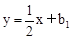 。
。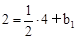 ,解得
,解得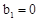 。∴直线MP的解析式为
。∴直线MP的解析式为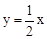 。
。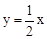 ,解得
,解得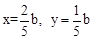 。
。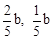 )。
)。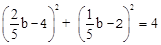 ,化简得
,化简得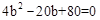 。
。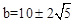 。
。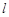 经过点A、B、C、D四点时b的值,从而分0≤b≤4,4<b≤6,6<b≤12,12<b≤14,b>14五种情况分别讨论即可。
经过点A、B、C、D四点时b的值,从而分0≤b≤4,4<b≤6,6<b≤12,12<b≤14,b>14五种情况分别讨论即可。

科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.(-5,3) | B.(1,3) | C.(1,-3) | D.(-5,-1) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.P在⊙A上 | B.P在⊙A外 | C.P在⊙A内 | D.以上答案都不对 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com