【题目】为了解居民用水情况，小明在某小区随机抽查了30户家庭的月用水量，结果如下表：
月用水量/m3 | 4 | 5 | 6 | 8 | 9 | 10 |
户数 | 6 | 7 | 9 | 5 | 2 | 1 |
则这30户家庭的月用水量的众数和中位数分别是（ ）
A.6，6
B.9，6
C.6，9
D.6，7
科目：初中数学 来源： 题型：
【题目】在□ABCD中，AC、BD交于点O，过点O作直线EF、GH，分别交平行四边形的四条边于E、G、F、H四点，连接EG、GF、FH、HE．
（1）如图①，试判断四边形EGFH的形状，并说明理由；
（2）如图②，当EF⊥GH时，四边形EGFH的形状是 ；
（3）如图③，在（2）的条件下，若AC=BD，四边形EGFH的形状是 ；
（4）如图④，在（3）的条件下，若AC⊥BD，试判断四边形EGFH的形状，并说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列各式：13=12 ， 13+23=32 ， 13+23+33=62 ， 13+23+33+43=102…
（1）请叙述等式左边各个幂的底数与右边幂的底数之间有什么关系？
（2）利用上述规律，计算：13+23+33+43+…+1003 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
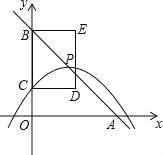
【题目】如图，在平面直角坐标系中，直线y=﹣x+4与x轴、y轴分别交于点A、B．抛物线
的顶点P在直线y=﹣x+4上，与y轴交于点C（点P、C不与点B重合），以BC为边作矩形BCDE，且CD=2，点P、D在y轴的同侧．
（1）n= （用含m的代数式表示），点C的纵坐标是 （用含m的代数式表示）．
（2）当点P在矩形BCDE的边DE上，且在第一象限时，求抛物线对应的函数表达式．
（3）设矩形BCDE的周长为d（d＞0），求d与m之间的函数表达式．
（4）直接写出矩形BCDE有两个顶点落在抛物线上时m的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】随着“互联网+”在各领域的延伸与融合，互联网移动医疗发展迅速，预计到2018年我国移动医疗市场规模将达到29150000000元，将29150000000用科学记数法表示为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为迎接“五一”劳动节，某中学组织了甲、乙两个义务劳动小组，甲组x人，乙组y人，到“中华路”和“青年路”打扫卫生，根据打扫卫生的进度，学校随时调整两组人数，如果从甲组调50人去乙组，则乙组人数为甲组人数的2倍；如果从乙组调m人去甲组，则甲组人数为乙组人数的3倍．
(1)求出x与m之间的函数表达式．
(2)问：当m为何值时，甲组人数最少，最少是多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】若关于x的一元二次方程x2﹣4x+m+2＝0有两个不相等实数根，且m为正整数，则此方程的解为（ ）
A. x1＝﹣1，x2＝3B. x1＝﹣1，x2＝﹣3
C. x1＝1，x2＝3D. x1＝1，x2＝﹣3
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD是正方形，BM=DF，AF垂直AM，M，B，C在一条直线上，且△AEM与△AEF恰好关于AE所在直线成轴对称，已知EF=x，正方形边长为y．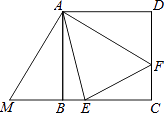 
（1）图中△ADF可以绕点按顺时针方向旋转°后能与△重合；
（2）用x、y的代数式表示△AEM与△EFC的面积．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
