练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．化简：$\frac{{a}^{2}-3a}{{a}^{2}+a}$÷$\frac{a-3}{{a}^{2}-1}$•$\frac{a+1}{a-1}$．

    分析 原式利用除法法则变形，约分即可得到结果．

    解答 解：原式=$\frac{a（a-3）}{a（a+1）}$•$\frac{（a+1）（a-1）}{a-3}$•$\frac{a+1}{a-1}$=（a-1）•$\frac{a+1}{a-1}$=a+1．

    点评 此题考查了分式的乘除法，分式乘除法的关键是约分，约分的关键是找出公因式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    10．已知a⊕b表示（a-b）÷（a+b），
    （1）计算：1⊕2；
    （2）计算：（-3）⊕（10⊕6）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

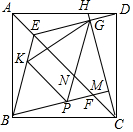    11．如图，四边形ABCD为正方形，H是AD上任意一点，连接CH，过B作BM⊥CH于M，交AC于F，过D作DE∥BM交AC于E，交CH于G，在线段BF上作PF=DG，连接PG，BE，其中PG交AC于N点，K为BE上一点，连接PK，KG，若∠BPK=∠GPK，CG=12，KP：EF=3：5，求$\frac{KG}{EG}$的值为$\frac{\sqrt{505}}{15}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．计算：
    （1）-13-（-22）+（-28）
    （2）-22-|-12|×（$\frac{2}{3}$-$\frac{3}{4}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

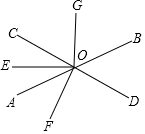    15．如图，直线AB与CD相交于O，OE是∠AOC的平分线，OF⊥CD，OG⊥OE，∠BOD=52°．
    （1）求∠AOF的度数；
    （2）求∠EOF与∠BOG是否相等？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．分式化简：
    （1）$\frac{-3ab}{{4{x^2}y}}÷\frac{21b}{10xy}$
    （2）$\frac{1}{{{{（x-y）}^2}}}+\frac{2}{{{x^2}-3xy+2{y^2}}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．如图（1），在△ABC中，点D、E分别在AB、AC上，连接DE，线段BE、CD相交于点O．
    （1）若∠DCB=∠EBC=$\frac{1}{2}$∠A，求证：$\frac{OC}{OD}$=$\frac{AB}{AE}$；
    （2）在（1）的条件下，求证：BD=CE；
    （3）如图（2），CD⊥AB，DE⊥AC，∠A=45°，BD=$\frac{1}{2}$CD，点M为DE中点，连接BM、CM，求证：BM⊥CM．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

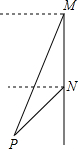    9．如图，轮船沿正南方向以30海里/时的速度匀速航行，在M处观测到灯塔P在西偏南68°方向上，航行2小时后到达N处，观测灯塔P在西偏南46°方向上，若该船继续向南航行至离灯塔最近位置，则此时轮船离灯塔的距离约为41.682（由科学计算器得到sin68°=0.9272，sin46°=0.7193，sin22°=0.3746，sin44°=0.6947）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．如图，拟从点A修建一条小径到边BC，若要使修建小径使用的材料最少，则过点A作AD⊥BC于点D，线段AD即为所求小径的位置，这样画的理由是垂线段最短．

    查看答案和解析>>

    同步练习册答案