
分析 (1)根据乘法交换律进行计算即可;
(2)先算括号里面的,再算除法即可;
(3)先算小括号里面的,再算除法即可;
(4)先算小括号里面的,再算中括号里面的,再算乘方,减法即可.
解答 解:(1)原式=[7$\frac{1}{9}$×(-$\frac{9}{4}$)]×(1$\frac{1}{2}$-1$\frac{1}{8}$+3$\frac{1}{4}$)
=(-16)×$\frac{3}{2}$-(-16)×(-$\frac{9}{8}$)+(-16)×$\frac{13}{4}$
=-24-18-52
=-94;
(2)原式=(-81+9)÷(-2)
=(-72)×(-$\frac{1}{2}$)
=36;
(3)原式=[$\frac{125}{8}$+$\frac{27}{8}$]÷(25+15+9)
=$\frac{152}{8}$÷49
=$\frac{152}{8}$×$\frac{1}{49}$
=$\frac{49}{49}$;
(4)原式=-52-[-8+(1-$\frac{3}{5}$)×(-$\frac{1}{2}$)]
=-52-[-8+$\frac{2}{5}$×(-$\frac{1}{2}$)]
=-52-[-8-$\frac{1}{5}$]
=-52+$\frac{41}{5}$
=-25+$\frac{41}{5}$
=-$\frac{84}{5}$.
点评 本题考查的是有理数的混合运算,在解答此题时要注意各种运算律的灵活应用.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
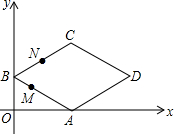 在平面直角坐标系中,四边形ABCD是菱形,其中点B的坐标是(0,2),点D的坐标是($4\sqrt{3}$,2),点M和点N是两个动点,其中点M从点B出发沿BA以每秒1个单位的速度做匀速运动,到点A后停止,同时点N从B点出发沿折线BC→CD以每秒2个单位的速度做匀速运动,如果其中一点停止运动,则另一点也停止运动.设M、N两点的运动时间为x,△BMN的面积是y,下列图象中能表示y与x的函数关系的图象大致是( )
在平面直角坐标系中,四边形ABCD是菱形,其中点B的坐标是(0,2),点D的坐标是($4\sqrt{3}$,2),点M和点N是两个动点,其中点M从点B出发沿BA以每秒1个单位的速度做匀速运动,到点A后停止,同时点N从B点出发沿折线BC→CD以每秒2个单位的速度做匀速运动,如果其中一点停止运动,则另一点也停止运动.设M、N两点的运动时间为x,△BMN的面积是y,下列图象中能表示y与x的函数关系的图象大致是( )| A. | 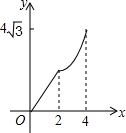 | B. | 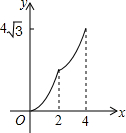 | C. | 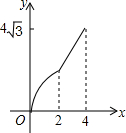 | D. | 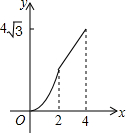 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com