
分析 (1)分式方程去分母转化为整式方程,表示出整式方程的解,由解为非负数求出k的范围,即可确定出正整数k的值;
(2)分式方程去分母转化为整式方程,分类讨论a的值,使分式方程无解即可.
解答 解:(1)去分母得:(x+k)(x-2)-k(x+2)=x2-4,
整理得:x=2-2k,
由x为非负数,得到2-2k≥0,即k≤1,
由k为正整数,得到k=1;
(2)去分母得:3-x-a(x-2)=-2,即(a+1)x=2a+5,
当a=-1时,显然方程无解;
当a≠-1时,x=$\frac{2a+5}{a+1}$,
当x=2时,a不存在;
当x=3时,a=2,
综上,a的值为-1,2.
点评 此题考查了分式方程的解,始终注意分式分母不为0这个条件.


 每课必练系列答案
每课必练系列答案科目:初中数学 来源: 题型:选择题
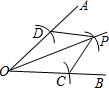 如图,用尺规作图画角平分线:以O为圆心,任意长为半径画弧交OA,OB于点C,D,再分别以C,D为圆心,以大于$\frac{1}{2}CD$长为半径画弧,两弧交于点P,由此得△POC≌△POD依据是( )
如图,用尺规作图画角平分线:以O为圆心,任意长为半径画弧交OA,OB于点C,D,再分别以C,D为圆心,以大于$\frac{1}{2}CD$长为半径画弧,两弧交于点P,由此得△POC≌△POD依据是( )| A. | AAS | B. | SAS | C. | SSS | D. | ASA |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正三角形,正方形 | B. | 正方形,正六边形 | ||
| C. | 正五边形,正六边形 | D. | 正六边形,正八边形 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30x+750>1080 | B. | 30x-750≥1080 | C. | 30x-750≤1080 | D. | 30x+750≥1080 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 项目 | 第一次锻炼 | 第二次锻炼 |
| 步数(步) | 10000 | ①10000(1+3x) |
| 平均步长(米/步) | 0.6 | ②0.6(1-x) |
| 距离(米) | 6000 | 7020 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com