
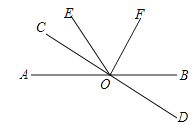
【题目】如图,直线AB和CD交于点O,∠COF=90°,OC平分∠AOE,∠COE=40°.
(1)求∠BOD的度数;
(2)OF平分∠BOE吗?请说明理由.
 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
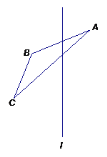
【题目】(1)小河的同旁有甲、乙两个村庄(左图),现计划在河岸AB上建一个水泵站,向两村供水,用以解决村民生活用水问题。(保留作图痕迹)
①如果要求水泵站到甲、乙两村庄的距离相等,水泵站M应建在河岸AB上的何处?
②如果要求建造水泵站,供水管道使用建材最省,水泵站N又应建在河岸AB上的何处?

(2)如图,作出△ABC关于直线l的对称图形;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)该玩具销售单价定为多少元时,商场能获得12000元的销售利润?
(2)该玩具销售单价定为多少元时,商场获得的销售利润最大?最大利润是多少?
(3)若玩具厂规定该品牌玩具销售单价不低于46元,且商场要完成不少于500件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
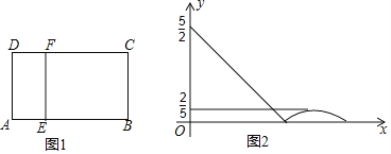
【题目】如图1,在矩形ABCD中,动点E从A出发,沿![]() 方向运动,当点E到达点C时停止运动,过点E做
方向运动,当点E到达点C时停止运动,过点E做![]() ,交CD于F点,设点E运动路程为x,
,交CD于F点,设点E运动路程为x, ![]() ,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是
,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是![]() ,则矩形ABCD的面积是( )
,则矩形ABCD的面积是( )
A. ![]() B.
B. ![]() C. 6 D. 5
C. 6 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
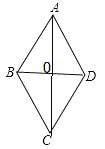
【题目】菱形ABCD中, ![]() ,其周长为32,则菱形面积为____________.
,其周长为32,则菱形面积为____________.
【答案】![]()
【解析】分析:根据菱形的性质易得AB=BC=CD=DA=8,AC⊥BD, OA=OC,OB=OD,再判定△ABD为等边三角形,根据等边三角形的性质可得AB=BD=8,从而得OB=4,在Rt△AOB中,根据勾股定理可得OA=4![]() ,继而求得AC=2AO=
,继而求得AC=2AO=![]() ,再由菱形的面积公式即可求得菱形ABCD的面积.
,再由菱形的面积公式即可求得菱形ABCD的面积.
详解:∵菱形ABCD中,其周长为32,
∴AB=BC=CD=DA=8,AC⊥BD, OA=OC,OB=OD,
∵![]() ,
,
∴△ABD为等边三角形,
∴AB=BD=8,
∴OB=4,
在Rt△AOB中,OB=4,AB=8,
根据勾股定理可得OA=4![]() ,
,
∴AC=2AO=![]() ,
,
∴菱形ABCD的面积为: ![]() =
=![]() .
.
点睛:本题考查了菱形性质:1.菱形的四个边都相等;2.菱形对角线相互垂直平分,并且每一组对角线平分一组对角;3.菱形面积公式=对角线乘积的一半.
【题型】填空题
【结束】
17
【题目】如图,在△ABC中, ![]() , AC=BC=3, 将△ABC折叠,使点A落在BC 边上的点D处,EF为折痕,若AE=2,则
, AC=BC=3, 将△ABC折叠,使点A落在BC 边上的点D处,EF为折痕,若AE=2,则![]() 的值为_____________.
的值为_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
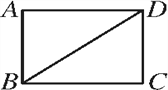
【题目】如图,BD是矩形ABCD的一条对角线.
(1)作BD的垂直平分线EF,分别交AD,BC于点E,F,垂足为点O;(要求用尺规作图,保留作图痕迹,不要求写作法)
(2)在(1)中,连接BE和DF,求证:四边形DEBF是菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
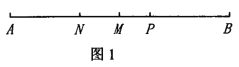
【题目】(1)如图1所示,已知线段AB=20cm,在AB上取一点P,M是AB的中点,N是AP中点,若MN=3cm,求线段AP的长;
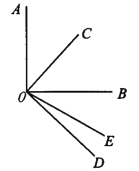
(2)如图2所示,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.则∠COE是多少度?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com