
【题目】在市举办的“划龙舟,庆端午”比赛中,甲、乙两队在比赛时的路程![]() (米)与时间
(米)与时间![]() (分钟)之间的函数关系图象如图所示,根据图象得到下列结论,你认为正确的结论是( )
(分钟)之间的函数关系图象如图所示,根据图象得到下列结论,你认为正确的结论是( )
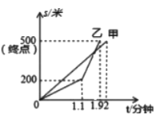
①这次比赛的全程是![]() 米;②乙队先到达终点;③比赛中两队从出发到
米;②乙队先到达终点;③比赛中两队从出发到![]() 分钟时间段,乙队的速度比甲队的速度快;④乙与甲相遇时乙的速度是
分钟时间段,乙队的速度比甲队的速度快;④乙与甲相遇时乙的速度是![]() 米/分钟;⑤在
米/分钟;⑤在![]() 分钟时,乙队追上了甲队.
分钟时,乙队追上了甲队.
A.①③④B.①②⑤C.①②④D.①②③④⑤
【答案】C
【解析】
由横纵坐标可直接判断①、②;观察图象比赛中两队从出发到1.1分钟时间段,乙队的图象在甲图象的下面可判断③;由图象得乙队在1.1至1.9分钟的路程为300米,可判断④;分别求出在1.8分钟时,甲队和乙队的路程,可判断⑤.
解:①由纵坐标看出,这次龙舟赛的全程是500m,故①正确;
②由横坐标可以看出,乙队先到达终点,故②正确;
③∵比赛中两队从出发到1.1分钟时间段,乙队的图象在甲图象的下面,
∴乙队的速度比甲队的速度慢,故③错误;
④∵由图象可知,乙队在1.1分钟后开始加速,加速的总路程是500-200=300(米),加速的时间是1.9-1.1=0.8(分钟),
∴乙与甲相遇时,乙的速度是300÷0.8=375(米/分钟),故④正确.
⑤甲队:500÷2×1.8=450(米),
乙队:200+(500-200)÷(1.9-1.1)×(1.8-1.1)=462.5(米),故⑤错误.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() 与一次函数y=k2x-k2+2在同一直角坐标系中的图象相交于A,B两点,其中A(-1,3),直线y=k2x-k2+2与坐标轴分别交于C,D两点,下列说法:①k1,k2<0;②点B的坐标为(3,-1);③当x<-1时,
与一次函数y=k2x-k2+2在同一直角坐标系中的图象相交于A,B两点,其中A(-1,3),直线y=k2x-k2+2与坐标轴分别交于C,D两点,下列说法:①k1,k2<0;②点B的坐标为(3,-1);③当x<-1时,![]() <k2x-k2+2;④tan∠OCD=-
<k2x-k2+2;④tan∠OCD=-![]() ,其中正确的是( )
,其中正确的是( )
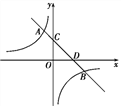
A. ①③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,线段EF过平行四边形ABCD的对角线的交点O,交AD于点E,交BC于点F。已知AB=4,BC=5,EF=3,那么四边形EFCD的周长是_____.
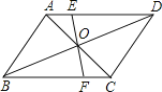
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是![]() 的切线,切点为A,AB是
的切线,切点为A,AB是![]() 的弦,过点B作
的弦,过点B作![]() ,交
,交![]() 于点C,连接AC,过点C作
于点C,连接AC,过点C作![]() ,交AD于点D,连接AO并延长AO交BC于点M,交
,交AD于点D,连接AO并延长AO交BC于点M,交![]() 于点E,交过点C的直线于点P,且
于点E,交过点C的直线于点P,且![]() .
.
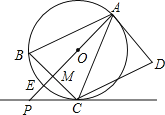
![]() 求证:
求证:![]() ;
;
![]() 判断直线PC与
判断直线PC与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
![]() 若
若![]() ,
,![]() ,求PC的长.
,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)若∠AOC=30°时,则∠DOE的度数为_____;
(2)将图①中的∠COD绕顶点O顺时针旋转至图②的位置,其它条件不变,探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
(3)将图①中的∠COD绕顶点O顺时针旋转至图③的位置,其他条件不变.直接写出∠AOC和∠DOE的度数之间的关系:_____.
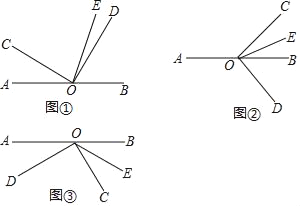
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展旅游经济,我市某景区对门票釆用灵活的售票方法吸引游客.门票定价为50元/人,非节假日打![]() 折售票,节假日按团队人数分段定价售票,即
折售票,节假日按团队人数分段定价售票,即![]() 人以下(含
人以下(含![]() 人)的团队按原价售票;超过
人)的团队按原价售票;超过![]() 人的团队,其中
人的团队,其中![]() 人仍按原价售票,超过
人仍按原价售票,超过![]() 人部分的游客打
人部分的游客打![]() 折售票.设某旅游团人数为
折售票.设某旅游团人数为![]() 人,非节假日购票款为
人,非节假日购票款为![]() (元),节假日购票款为
(元),节假日购票款为![]() (元).
(元).![]() 与
与![]() 之间的函数图象如图所示.
之间的函数图象如图所示.
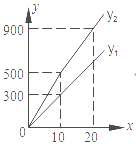
(1)观察图象可知:![]() ;
;![]() ;
;![]() ;
;
(2)直接写出![]() ,
,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)某旅行社导游王娜于5月1日带![]() 团,5月20日(非节假日)带
团,5月20日(非节假日)带![]() 团都到该景区旅游,共付门票款1900元,
团都到该景区旅游,共付门票款1900元,![]() ,
,![]() 两个团队合计50人,求
两个团队合计50人,求![]() ,
,![]() 两个团队各有多少人?
两个团队各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:点![]() 在同一条直线上,点
在同一条直线上,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 的中点.
的中点.
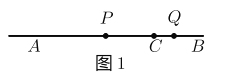
(1)如图1 ,当点![]() 在线段
在线段![]() 上时.
上时.
①若![]() ,则线段
,则线段![]() 的长为_______.
的长为_______.
②若点![]() 为线段
为线段![]() 上任意一点,
上任意一点, ![]() ,则线段
,则线段![]() 的长为_______. ( 用含
的长为_______. ( 用含![]() 的代数式表示)
的代数式表示)
(2)如图2 ,当点![]() 不在线段
不在线段![]() 上时,若
上时,若![]() ,求
,求![]() 的长(用含
的长(用含![]() 的代数式表示) .
的代数式表示) .
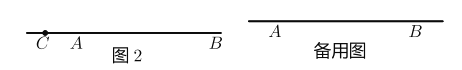
(3)如图,已知![]() ,作射线
,作射线![]() ,若射线
,若射线![]() 平分
平分![]() ,射线
,射线![]() 平分
平分![]() .
.
①当射线![]() 在
在![]() 的内部时,则
的内部时,则![]() =________°.
=________°.
②当射线![]() 在
在 ![]() 的外部时,则
的外部时,则![]() =_______°. ( 用含
=_______°. ( 用含![]() 的代数式表示) .
的代数式表示) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MAN=120°,AC平分∠MAN.B、D分别在射线AN、AM上.
(1)在图1中,当∠ABC=∠ADC=90°时,求证:AD+AB=AC
(2)若把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,如图2所示,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.

(图1) (图2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com