
【题目】在横线上填写理由,完成下面的证明. 如图,已知∠1+∠2=180°,∠B=∠3,求证∠C=∠AED
证明:∵∠1+∠2=180°(已知),∠1+∠DFE=180°()
∴∠2=∠DFE()
∴AB∥EF()
∴∠3=∠ADE()
又∵∠B=∠3(已知)
∴∠B=∠ADE()
∴DE∥BC()
∴∠C=∠AED()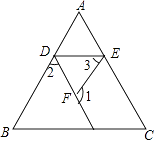
【答案】邻补角定义;同角的补角相等;内错角相等,两直线平行;两直线平行,内错角相等;等量代换;同位角相等,两直线平行;两直线平行,同位角相等.
【解析】证明:∵∠1+∠2=180°(已知),∠1+∠DFE=180°(邻补角定义), ∴∠2=∠DFE(同角的补角相等),
∴AB∥EF(内错角相等,两直线平行),
∴∠3=∠ADE(两直线平行,内错角相等),
又∵∠B=∠3(已知),
∴∠B=∠ADE(等量代换)
∴DE∥BC(同位角相等,两直线平行),
∴∠C=∠AED(两直线平行,同位角相等),
所以答案是:邻补角定义,同角的补角相等,内错角相等,两直线平行,两直线平行,内错角相等,等量代换,同位角相等,两直线平行,两直线平行,同位角相等.
【考点精析】关于本题考查的平行线的判定与性质,需要了解由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美结合.研究数轴我们发现有许多重要的规律:
例如,若数轴上![]() 点、
点、![]() 点表示的数分别为
点表示的数分别为![]() 、
、![]() ,则
,则![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ,线段
,线段![]() 的中点
的中点![]() 表示的数为
表示的数为![]() .
.
(问题情境)
在数轴上,点![]() 表示的数为-20,点
表示的数为-20,点![]() 表示的数为10,动点
表示的数为10,动点![]() 从点
从点![]() 出发沿数轴正方向运动,同时,动点
出发沿数轴正方向运动,同时,动点![]() 也从点
也从点![]() 出发沿数轴负方向运动,已知运动到4秒钟时,
出发沿数轴负方向运动,已知运动到4秒钟时,![]() 、
、![]() 两点相遇,且动点
两点相遇,且动点![]() 、
、![]() 运动的速度之比是
运动的速度之比是![]() (速度单位:单位长度/秒).
(速度单位:单位长度/秒).
![]()
![]()
备用图
(综合运用)
(1)点![]() 的运动速度为______单位长度/秒,点
的运动速度为______单位长度/秒,点![]() 的运动速度为______单位长度/秒;
的运动速度为______单位长度/秒;
(2)当![]() 时,求运动时间;
时,求运动时间;
(3)若点![]() 、
、![]() 在相遇后继续以原来的速度在数轴上运动,但运动的方向不限,我们发现:随着动点
在相遇后继续以原来的速度在数轴上运动,但运动的方向不限,我们发现:随着动点![]() 、
、![]() 的运动,线段
的运动,线段![]() 的中点
的中点![]() 也随着运动.问点
也随着运动.问点![]() 能否与原点重合?若能,求出从
能否与原点重合?若能,求出从![]() 、
、![]() 相遇起经过的运动时间,并直接写出点
相遇起经过的运动时间,并直接写出点![]() 的运动方向和运动速度;若不能,请说明理由.
的运动方向和运动速度;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】a、b是给定的整数,某同学分别计算x=-1,1,2,4时代数式ax+b的值,依次得到下列四个结果,已知其中3个是正确的,那么错误的是( )
A. ![]() B. a+b=5 C. 2a+b=7 D. 4a+b=14
B. a+b=5 C. 2a+b=7 D. 4a+b=14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,射线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF。
(1)求∠EOB的度数;
(2)若平行移动AB,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值;
(3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:3+2![]() =(1+
=(1+![]() )2,善于思考的小明进行了以下探索:
)2,善于思考的小明进行了以下探索:
设a+b=(m+n![]() )2(其中a、b、m、n均为整数),则有a+b
)2(其中a、b、m、n均为整数),则有a+b![]() =m2+2n2+2mn
=m2+2n2+2mn![]() .
.
∴a=m2+2n2,b=2mn.这样小明就找到了一种把部分a+b![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b![]() =(m+n
=(m+n![]() )2,用含m、n的式子分别表示a、b,得a= ,b= ;
)2,用含m、n的式子分别表示a、b,得a= ,b= ;
(2)试着把7+4![]() 化成一个完全平方式.
化成一个完全平方式.
(3)若a是216的立方根,b是16的平方根,试计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两座城市的中心火车站A,B两站相距360 km.一列动车与一列特快列车分别从A,B两站同时出发相向而行,动车的平均速度比特快列车快54 km/h,当动车到达B站时,特快列车恰好到达距离A站135 km处的C站.求动车和特快列车的平均速度各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
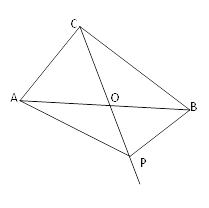
【题目】如图,在△ABC中,AB=2,AO=BO,P是直线CO上的一个动点,∠AOC=60°,当△PAB是以BP为直角边的直角三角形时,AP的长为( )
A. ![]() ,1,2 B.
,1,2 B. ![]() ,
,![]() ,2 C.
,2 C. ![]() ,
,![]() ,1 D.
,1 D. ![]() ,2
,2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平面内有两条直线AB、CD,且AB∥CD,P为一动点. 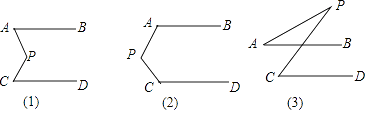
(1)当点P移动到AB、CD之间时,如图(1),这时∠P与∠A、∠C有怎样的关系?证明你的结论;
(2)当点P移动到图(2)、图(3)的位置时,∠P、∠A、∠C又有怎样的关系?请分别写出你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
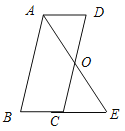
【题目】已知:如图,平行四边形 ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD ≌ △EOC;
(2)连接AC,DE,当∠B![]() ∠AEB
∠AEB![]() _______ °时,四边形ACED是正方形?请说明理由.
_______ °时,四边形ACED是正方形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com