

分析 (1)①由平行线的性质得出∠EBP=∠ACB,由已知条件得出∠PEB=∠ABC,由等腰三角形的性质得出∠ABC=∠ACB,因此∠EBP=∠PEB,即可得出结论;
②证出∠EPD=∠BPA,由ASA证明△APB≌△DPE即可;
(2)连接AD,由全等三角形的性质得出PA=PD,证出∠PDA=∠ACB=∠ABC,由于DB∥AC,由平行线的性质和角的关系得出∠PDA=∠PMC,因此∠PMA+∠PDA=180°,得出四边形AMPD四点共圆,由圆周角相等得出∠APD=∠AMD=∠BAC,由平行线的性质得出∠DBQ=∠BAC,∠BDQ=∠AMD,得出∠BDQ=∠DBQ,即可得出结论.
解答 (1)证明:①∵DB∥AC,
∴∠EBP=∠ACB,
∵∠BAC=∠BPE,
∴∠PEB=∠ABC,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠EBP=∠PEB,
∴PB=PE;
②∵∠APD=∠BPE,
∴∠EPD=∠BPA,
在△APB和△DPE中,
$\left\{\begin{array}{l}{∠EPD=∠BPA}\\{PE=PB}\\{∠PEB=∠ABC}\end{array}\right.$,
∴△APB≌△DPE(ASA);
(2)证明: 连接AD,如图所示:
连接AD,如图所示:
∵△APB≌△DPE,
∴PA=PD,
∴∠PAD=∠PDA,
∵∠BAC=∠APD,
∴∠PDA=∠ACB=∠ABC,
∵DB∥AC,
∴∠PEB=∠PMC,
∵∠PEB=∠ABC,
∴∠PDA=∠PMC,
∴∠PMA+∠PDA=180°,
∴四边形AMPD四点共圆,
∴∠APD=∠AMD=∠BAC,
∵DB∥AC,
∴∠DBQ=∠BAC,∠BDQ=∠AMD,
∴∠BDQ=∠DBQ,
∴DQ=BQ,
∴△BQD是等腰三角形.
点评 本题考查了全等三角形的判定与性质、等腰三角形的判定与性质、平行线的性质、四点共圆、圆周角定理等知识;本题综合性强,有一定难度,特别是(2)中,需要通过证明四点共圆,运用圆周角定理才能得出结论.


 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AB=AC=6,F为BC的中点,D为CA延长线上一点,∠DFE=∠B.
如图,△ABC中,AB=AC=6,F为BC的中点,D为CA延长线上一点,∠DFE=∠B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
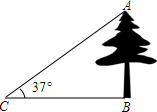 如图,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为37°,BC=20m,则树的高度AB为( )
如图,在一次数学课外实践活动中,小文在点C处测得树的顶端A的仰角为37°,BC=20m,则树的高度AB为( )| A. | 20m | B. | 15m | C. | 12m | D. | 16m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE,连结BF,CE.
如图,在△ABC中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE,连结BF,CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
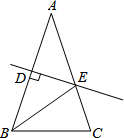 如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )
如图,等腰△ABC中,AB=AC=8,BC=5,AB的垂直平分线DE交AB于点D,交AC于点E,则△BEC的周长为( )| A. | 13 | B. | 14 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y2<y1<y3 | C. | y3<y2<y1 | D. | y3<y1<y2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com