
����Ŀ����֪������y��mx2+2mx+n��x���һ������ΪA����3��0������y��ĸ����ύ�ڵ�C��

��1��ֱ��д�������ߵĶԳ��ᣬ����������x�����һ������B�����ꣻ
��2����C����x��ĶԳƵ�Ϊ��D������D����ABΪֱ���İ�Բ��ʱ���������ߵĽ���ʽ��
��3���ڣ�2��������£������������Ƿ����һ��P��ʹBP��BD��AB����֮�У�����һ�������������нǵĽ�ƽ���ߣ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��x����1����B��1��0������2��y��![]() x2+
x2+![]() x��
x��![]() ����3����P����������0����
����3����P����������0����![]() ����4��
����4��![]() ����
����
��������
��1�������ĶԳ���Ϊ��x=-![]() =-1����A��-3��0�������B��1��0����
=-1����A��-3��0�������B��1��0����
��2����BE=ED����4=1+n2����ã�n=-![]() ����ֵ����ȥ�����ʵ�C��0��-
����ֵ����ȥ�����ʵ�C��0��-![]() ����������⣻
����������⣻
��3����AB�ǽ�ƽ���ߡ�BP�ǽ�ƽ���ߡ�BD�ǽ�ƽ��������������ֱ���⼴�ɣ�
��1�������ĶԳ���Ϊ��x����![]() ����1��
����1��
��A����3��0�������B��1��0����
��2����C��0��n�������D��0����n����
��Բ��Բ��ΪE����1��0����

��BE��ED����4��1+n2����ã�n����![]() ����ֵ����ȥ����
����ֵ����ȥ����
�ʵ�C��0����![]() ����
����
�������ߵı���ʽΪ��y��a��x+3����x��1����a��x2+2x��3����
����3a����![]() ����ã�a��
����ã�a��![]() ��
��
�������ߵı���ʽΪ��y��![]() x2+
x2+![]() x��
x��![]() ���٣�
���٣�
��3���ٵ�AB�ǽ�ƽ����ʱ��
���ڵ�D��C����x��Գƣ��ʵ�C��Ϊ��P��0����![]() ����
����
�ڵ�BP�ǽ�ƽ����ʱ��
����OD��![]() ��OB��1���ʡ�DBA��60�㣬��BP����б��Ϊ30�㣬
��OB��1���ʡ�DBA��60�㣬��BP����б��Ϊ30�㣬
��ֱ��BP�ı���ʽΪ��y����![]() x+b������B�����������ʽ����ã�b��
x+b������B�����������ʽ����ã�b��![]() ��
��
��ֱ��BP�ı���ʽΪ��y����![]() x+
x+![]() ���ڣ�
���ڣ�
�����٢ڲ���ã�x����4��1����ȥ1�����ʵ�P����4��![]() ����
����
�۵�BD�ǽ�ƽ����ʱ��
ͬ����P��m��![]() m��
m��![]() ����
����
����P����������ʽ����ã�x��0��1����ȥ����
���ϣ���P������Ϊ����0����![]() ����4��
����4��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��ʶ������ABC�У���A����B����C���Եı߷ֱ���a��b��c��ʾ�����һ�������ε�һ���ڽǵ�����һ���ڽǵ�2�������dz�������������Ϊ�����������Ρ���
��1��������֤����ͼ1������ABC�У���a��![]() ��b��1��c��2����֤����ABCΪ���������Σ�
��b��1��c��2����֤����ABCΪ���������Σ�
��2��ģ��̽������ͼ2����������ı��������Σ�����A��2��B����֤��a2��b��b+c��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������Ǻ��������µĹ�ʽ��
��cos����+������cos��cos����sin��sin����sin����+������sin��cos��+cos��sin����
��tan����+������![]() ��
��
��������Щ��ʽ���Խ�һЩ��������ǵ����Ǻ���ת��Ϊ����ǵ����Ǻ�������ֵ����tan105�㣽tan��45��+60�㣩��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
���������֪ʶ�������ѡ���ʵ��Ĺ�ʽ��������ʵ�����⣺
��1����cos75���ֵ��
��2����ͼ��ֱ������һ������CD�Ϸ��ĵ�A����ý����ﶥ�˵�D�ĸ�����Ϊ60�㣬�˵�C�ĸ�����Ϊ75�㣬��ʱֱ�����뽨����CD��ˮƽ����BCΪ42m��������CD�ĸߣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪���κ���������B��3��0����C��0��3����D��4��-5��
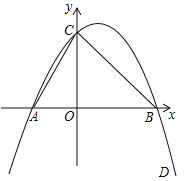
��1���������ߵĽ���ʽ��
��2������ABC�������
��3����P����������һ������S��ABP=![]() S��ABC�������ĵ�P�м�����ֱ��д�����ǵ�������
S��ABC�������ĵ�P�м�����ֱ��д�����ǵ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ��κ���![]() ������˵��������ǣ� ��
������˵��������ǣ� ��
A.��![]() ʱ��
ʱ��![]() ��
��![]() ���������СB.����ͼ����
���������СB.����ͼ����![]() ���н���
�����
C.��![]() ʱ��
ʱ��![]() D.����ͼ����
D.����ͼ����![]() �ύ�ڵ�
�ύ�ڵ�![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ��������ߵĵ������ǹ����µ���������ͼ��ʾ���µ�������ABΪ610�ף�Զ����һ����¥��ij����¥��C���������B������Ϊ45������¥��D���������B������Ϊ39����
��1�����¥�������֮��ľ���AC��
��2�����¥�ĸ߶�CD����ȷ��1�ף���
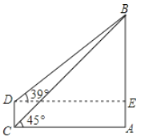
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����-3��-1��![]() ��1��3��������У������ȡһ��������Ϊa�������x��һ�κ���y=-x+a��ͼ����������Χ�������ε����������4�ĸ���Ϊ______��
��1��3��������У������ȡһ��������Ϊa�������x��һ�κ���y=-x+a��ͼ����������Χ�������ε����������4�ĸ���Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ͼ����3�����ҹ�������ѧ����ˬ��ע�⡶�����㾭��ʱ�����ģ����dz���Ϊ����ˬ��ͼ������֪AE=3��BE=2������������ABCD������Ͷ�����ڣ�ÿ�ξ�����������ABCD�ڣ�������������ABCD���κ�һ��Ļ�����ȣ�����ǡ������������EFGH�ڵĸ���Ϊ_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������㳡��Ҫ����һ��Բ�ε���ˮ�أ�����ˮ�����봹ֱ��װһ������![]() �����Ӷ���
�����Ӷ���![]() ��װ����ͷ����
��װ����ͷ����![]() �����������ˮ�����ڸ��������ϣ�����״��ͬ��������·�����£���ͼ��ʾ��������֪
�����������ˮ�����ڸ��������ϣ�����״��ͬ��������·�����£���ͼ��ʾ��������֪![]() �ף������ˮ������ߵ�
�ף������ˮ������ߵ�![]() ��ˮƽ��ĸ߶���
��ˮƽ��ĸ߶���![]() �ף�������
�ף�������![]() �ľ���Ϊ
�ľ���Ϊ![]() �ף�
�ף�
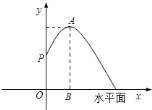
![]() �����������ߵĽ���ʽ��
�����������ߵĽ���ʽ��
![]() �������������أ�ˮ�صİ뾶����Ҫ�����ף�����ʹ�����ˮ�����������ڳ��⣿
�������������أ�ˮ�صİ뾶����Ҫ�����ף�����ʹ�����ˮ�����������ڳ��⣿
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com