练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    计算
    （1）一个等腰三角形的一边长为8cm，周长为20cm．求：其它两边的长．
    （2）一个多边形的内角和为1800°，并且这个多边形的各个内角都相等，求：这个多边形每一个内角的度数．
    分析：（1）已知条件中，本题没有明确说明已知的边长是否是腰长，所以有两种情况讨论，还应判定能否组成三角形．
    （2）先根据多边形的内角和公式（n-2）•180°求出多边形的边数，然后利用内角和除以边数即可；
    解答：解：（1）①底边长为8，则腰长为：（20-8）÷2=6，所以另两边的长为6cm，6cm，能构成三角形；
    ②腰长为8，则底边长为：20-8×2=4，底边长为8cm，另一个腰长为4cm，能构成三角形．
    因此另两边长为8cm、4cm或6cm、6cm．

    （2）解：设多边形的边数为n，
    则（n-2）•180°=1800°，
    解得n=12，
    1800°÷12=150°．
    这个多边形的每一个内角都等于150°．
    点评：本题考查了多边形的内角与外角及等腰三角形的性质，熟记内角和公式求出多边形的边数是解题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    在数学的学习中，我们要学会总结，不断地归纳，思考和运用，这样才能提高我们解决问题的能力，下面这个问题大家一定似曾相识：
    （1）比较大小：
    ①2+1
     
    2
    		2×1
    ；  ②3+
    1
    3
     
    2
    		3×
    1
    3
    ③8+8
     
    2
    		8×8

    通过上面三个计算，我们可以初步对任意的非负实数a，b做出猜想a+b
     
    2
    		ab
    ；
    （2）学习了《二次根式》后我们可以对此猜想进行代数证明，请欣赏：
    对于任意非负实数a，b，∵(
    		a
    -
    		b
    )2≥0    ，∴a-2
    		ab
    +b≥0    ，∴a+b≥2
    		ab
    ，只有当a=b时，等号成立．
    （3）学习《圆》后，我们可以对这个结论进行几何验证：
    如图，AB为半圆O的直径，C为半圆上的任意一点，（与A、B不重合）过点C作CD⊥AB，垂足为D，AD=a，DB=b．
    根据图形证明：a+b≥2
    		ab
    ，并指出等号成立时的条件．
    精英家教网
    （4）蓦然回首，我们发现在上学期的《梯形的中位线》一节遇到的一个问题，此时运用这个结论解决是那样的简单：
    如图有一个等腰梯形工件（厚度不计），其面积为1800cm2，现在要用细包装带如图那样包扎（四点为四边中点），则至少需要包装带的长度为
     
    cm．
    （注意：包扎时背面也有带子，打结处长度忽略不计）
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在数学的学习中，我们要学会总结，不断地归纳，思考和运用，这样才能提高我们解决问题的能力，下面这个问题大家一定似曾相识：
    （1）比较大小：
        ①2+1
    ＞
    ＞
    		2×1
    ；   ②3+
    1
    3
    ＞
    ＞
    2
    		3×
    1
    3
    ；   ③8+8
    =
    =
    2
    		8×8
    ；
    （2）通过上面三个计算，我们可以初步对任意的非负实数a，b做出猜想  a+b
    ≥
    ≥
    2
    		ab
    ；
    （3）蓦然回首，我们发现在《梯形的中位线》一节遇到的一个问题，此时运用这个结论巧妙解决；如图有一个等腰梯形工件（厚度不计），其面积为1800cm2，现在要用细包装带如图那样包扎（四点为四边中点），则至少需要包装带的长度为
    120
    		2
    120
    		2
    cm．

    查看答案和解析>>

    科目：初中数学 来源：2012届江苏省江阴初级中学九年级5月中考模拟数学试卷（带解析） 题型：解答题

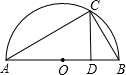
    如图，以OA1＝2为底边做等腰三角形，使得第三个顶点C1恰好在直线y=x+2上，并以此向左、右依次类推，作一系列底边为2，第三个顶点在直线y=x+2上的等腰三角形．
    （1）请你通过计算说明：底边为2，顶点在直线y=x+2上且面积为21的等腰三角形位于图
    中什么位置？
    （2）求证：y轴右侧的每一个等腰三角形的面积都等于前后两个以腰为一边的三角形面积之和的一半（如：S右1=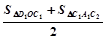，S右2=）．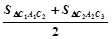
    （3）过D1、A1、C2三点画抛物线．问在抛物线上是否存在点P，使得△PD1C2的面积是△C1OD1与△C1A1C2面积和的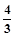．若存在，请求出点P的坐标；若不存在，请说明理由．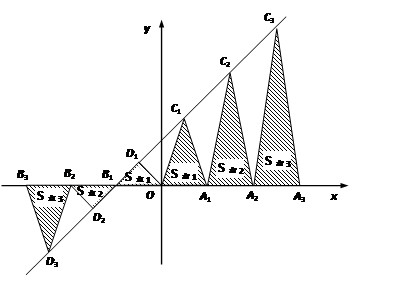

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年江苏省九年级5月中考模拟数学试卷（解析版） 题型：解答题

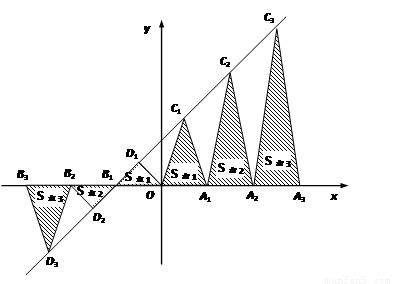
    如图，以OA1＝2为底边做等腰三角形，使得第三个顶点C1恰好在直线y=x+2上，并以此向左、右依次类推，作一系列底边为2，第三个顶点在直线y=x+2上的等腰三角形．

    （1）请你通过计算说明：底边为2，顶点在直线y=x+2上且面积为21的等腰三角形位于图

    中什么位置？

    （2）求证：y轴右侧的每一个等腰三角形的面积都等于前后两个以腰为一边的三角形面积之和的一半（如：S右1=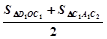，S右2=）．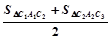

    （3）过D1、A1、C2三点画抛物线．问在抛物线上是否存在点P，使得△PD1C2的面积是△C1OD1与△C1A1C2面积和的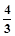．若存在，请求出点P的坐标；若不存在，请说明理由．

     

    查看答案和解析>>

    科目：初中数学 来源：2009-2010学年江苏省无锡市育才中学九年级（上）期中数学试卷（解析版） 题型：解答题

    在数学的学习中，我们要学会总结，不断地归纳，思考和运用，这样才能提高我们解决问题的能力，下面这个问题大家一定似曾相识：
    （1）比较大小：
    ①2+1______；  ②______③8+8______
    通过上面三个计算，我们可以初步对任意的非负实数a，b做出猜想a+b______；
    （2）学习了《二次根式》后我们可以对此猜想进行代数证明，请欣赏：
    对于任意非负实数a，b，∵，∴，∴，只有当a=b时，等号成立．
    （3）学习《圆》后，我们可以对这个结论进行几何验证：
    如图，AB为半圆O的直径，C为半圆上的任意一点，（与A、B不重合）过点C作CD⊥AB，垂足为D，AD=a，DB=b．
    根据图形证明：，并指出等号成立时的条件．

    （4）蓦然回首，我们发现在上学期的《梯形的中位线》一节遇到的一个问题，此时运用这个结论解决是那样的简单：
    如图有一个等腰梯形工件（厚度不计），其面积为1800cm2，现在要用细包装带如图那样包扎（四点为四边中点），则至少需要包装带的长度为______

    查看答案和解析>>

    同步练习册答案