C
分析:根据一元二次方程根与系数的关系可得:α+β=3,α
2+β
2=(α+β)
2-2αβ=3
2-2×(-2)=13,α
2β
2=(αβ)
2=(-2)
2=4,则可以写出α
2、β
2为根的一元二次方程.而利用一元二次方程根的判别式可以判定方程根的情况.
解答:A、根据一元二次方程根与系数的关系可得:α+β=3,故A正确.
B、∴△=b
2-4ac=(-3)
2-4×1×(-2)=17>0,故一元二次方程有两个不等实数根,所以α≠β,故B正确.
C、根据一元二次方程根与系数的关系可得:α+β=3,αβ=-2,所以

,故C错误.
D、α
2+β
2=(α+β)
2-2αβ=3
2-2×(-2)=13,α
2β
2=(αβ)
2=(-2)
2=4,所以以α
2、β
2为根的一元二次方程是y
2-13y+4=0,故D正确.
故选C.
点评:本题综合考查了一元二次方程根与系数的关系和根的判别式,题目典型,综合性较强,是一道很好的题目.

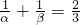
 ,故C错误.
,故C错误.
