
【题目】如图,AB是⊙O的直径,NM与⊙O相切于点M,与AB的延长线交于点N,MH⊥AB于点H.
(1)求证:∠1=∠2;
(2)若∠N=30°,BN=5,求⊙O的半径;
(3)在(2)的条件下,求线段BN、MN及劣弧BM围成的阴影部分面积.
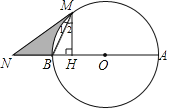
【答案】(1)详见解析;(2)⊙O的半径为5;(3)![]()
【解析】
(1)根据切线的性质得出OM⊥MN,即可得出∠1+∠BMO=∠NMO=90°,由NH⊥AB,推出∠2+∠MBO=90°,根据等腰三角形的性质得出∠OBM=∠OMB,即可证得∠1=∠2;
(2)由∠N=30°,推出∠1+∠2=60°,所以∠1=∠2=30°,∠MON=60°,得到BM=BN=5,易知△OBM为等边三角形,所以OB=OM=BM=5,得出结论;
(3)三角形OMN的面积减去扇形OMN的面积即为线段BN、MN及劣弧BM围成的阴影部分面积.
解:(1)证明:连接OM,
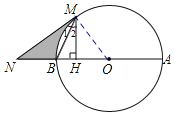
∵NM与⊙O相切,
∴OM⊥MN,
∵OB=OM,
∴∠OBM=∠OMB,
∵NH⊥AB,
∴∠2+∠MBO=90°,
∵∠1+∠BMO=∠NMO=90°,
∴∠1=∠2;
(2)∵∠N=30°,
MH⊥AB,
∴∠1+∠2=60°,
∴∠1=∠2=30°,∠MON=60°,
∴BM=BN=5,
∵OB=OM,
∴△OBM为等边三角形,
∴OB=OM=BM=5,
即⊙O的半径为5;
(3)由(2)知,∠N=30°,OM=5,
∴MN=5![]() ,
,
∴S△OMN=![]() MNOM=
MNOM=![]() =
=![]() ,
,
S扇形MOB=![]() =
=![]() ,
,
∴线段BN、MN及劣弧BM围成的阴影部分面积=![]() .
.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】如图是抛物线![]() 图象的一部分,抛物线的顶点是
图象的一部分,抛物线的顶点是![]() ,对称轴是直线
,对称轴是直线![]() ,且抛物线与
,且抛物线与![]() 轴的一个交点为
轴的一个交点为![]() ;直线
;直线![]() 的解析式为
的解析式为![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③方程
;③方程![]() 有两个不相等的实数根;④抛物线与
有两个不相等的实数根;④抛物线与![]() 轴的另一个交点是
轴的另一个交点是![]() ;⑤当
;⑤当![]() 时,则
时,则![]() .其中正确的是( )
.其中正确的是( )
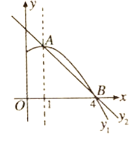
A.①②B.①③⑤C.①④D.①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点E,F分别在AD,BC上,且AE=DE,BC=3BF,连接EF,将矩形ABCD沿EF折叠,点A恰好落在BC边上的点G处,则cos∠EGF的值为_____.
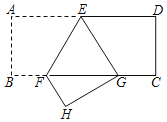
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】移动支付快捷高效,中国移动支付在世界处于领先水平,为了解人们平时最喜欢用哪种,移动支付支付方式,为此在某步行街,使用某app,软件对使用移动支付的行人进行随机抽样调查,设置了四个选项,支付宝,微信,银行卡,其他移动支付(每人只选一项),以下是根据调查结果分别整理的不完整的条形统计图和扇形统计图.
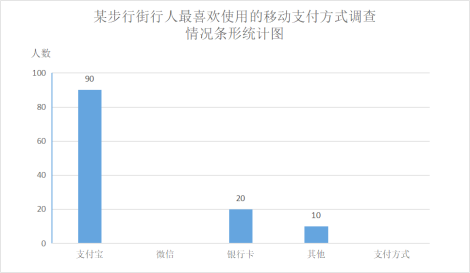

请你根据下列统计图提供的信息,完成下列问题.
(1)这次调查的样本容量是 ;
(2)请补全条形统计图;
(3)求在此次调查中表示使用微信支付的扇形所对的圆心角的度数.
(4)若某天该步行街人流量为10万人,其中40%的人购物并选择移动支付,请你依据此次调查获得的信息,估计一下当天使用银行卡支付的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
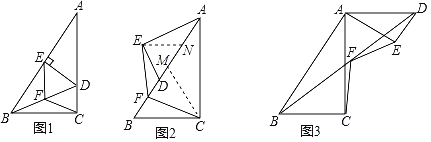
【题目】如图1,△ABC是直角三角形,∠ACB=90°,点D在AC上,DE⊥AB于E,连接BD,点F是BD的中点,连接EF,CF.
(1)EF和CF的数量关系为 ;
(2)如图2,若△ADE绕着点A旋转,当点D落在AB上时,小明通过作△ABC和△ADE斜边上的中线CM和EN,再利用全等三角形的判定,得到了EF和CF的数量关系,请写出此时EF和CF的数量关系 ;
(3)若△AED继续绕着点A旋转到图3的位置时,EF和CF的数量关系是什么?写出你的猜想,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
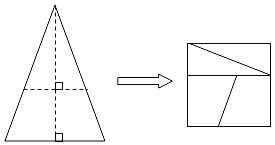
【题目】如图,将等腰三角形纸片沿图中虚线剪成四块图形,用这四块图形进行拼接,恰能拼成一个没有缝隙的正方形,则正方形的边长与等腰三角形的底边长的比为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
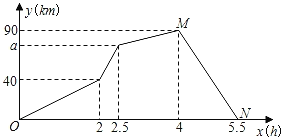
【题目】某快递公司有甲、乙两辆货车沿同一路线从A地到B地配送货物.某天两车同时从A地出发,驶向B地,途中乙车由于出现故障,停车修理了一段时间,修理完毕后,乙车加快了速度匀速驶向B地;甲车从A地到B地速度始终保持不变.如图所示是甲、乙两车之间的距离y(km)与两车出发时间x(h)的函数图象.根据相关信息解答下列问题:
(1)点M的坐标表示的实际意义是什么?
(2)求出MN所表示的关系式,并写出乙故障后的速度;
(3)求故障前两车的速度以及a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AB=5cm,cosB![]() .动点D从点A出发沿着射线AC的方向以每秒1cm的速度移动,动点E从点B出发沿着射线BA的方向以每秒2cm的速度移动.已知点D和点E同时出发,设它们运动的时间为t秒.联结BD.
.动点D从点A出发沿着射线AC的方向以每秒1cm的速度移动,动点E从点B出发沿着射线BA的方向以每秒2cm的速度移动.已知点D和点E同时出发,设它们运动的时间为t秒.联结BD.
(1)当AD=AB时,求tan∠ABD的值;
(2)以A为圆心,AD为半径画⊙A;以点B为圆心、BE为半径画⊙B.讨论⊙A与⊙B的位置关系,并写出相对应的t的值.
(3)当△BDE为直角三角形时,直接写出tan∠CBD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从青岛到济南有南线和北线两条高速公路:南线全长400千米,北线全长320千米.甲、乙两辆客车分别由南线和北线从青岛驶往济南,已知客车甲在南线高速公路上行驶的平均速度比客车乙在北线高速公路上快20千米/小时,两车恰好同时到达济南,求两辆客车从青岛到济南所用的时间是多少小时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com