
 ,且
,且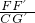 =
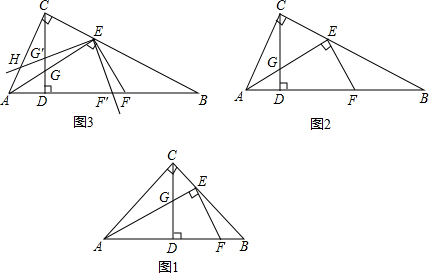
=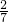 ,求线段G′H的长.
,求线段G′H的长.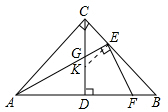 (1)证明:在Rt△ABC中,tan∠BAC=1=tan45°,
(1)证明:在Rt△ABC中,tan∠BAC=1=tan45°,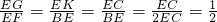 ,
,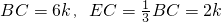 ,
,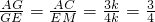
 =
= ,
, ,∴
,∴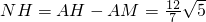
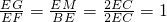 ,
,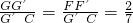 .
. ,
, ,
, ,
,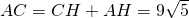 ,
,
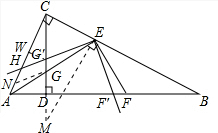
 ,
, ,
,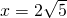 ,
,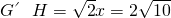 .
.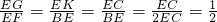 ,即可得出EF=2EG;
,即可得出EF=2EG;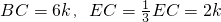 ,再过点E作EM⊥BC,EM与CD的延长线相交于点M,得出△AGC∽△EGM,得出
,再过点E作EM⊥BC,EM与CD的延长线相交于点M,得出△AGC∽△EGM,得出 ,再过点G作GN∥EH,与AH相交于点N,得出△ANG∽△AHE,得出NH的值,同理得出△GEM∽△FEB,得出EF=EG.同理可证EF′=EG′,∠FEF'=∠GEG',得出△GEG'≌△FEF',即可证出
,再过点G作GN∥EH,与AH相交于点N,得出△ANG∽△AHE,得出NH的值,同理得出△GEM∽△FEB,得出EF=EG.同理可证EF′=EG′,∠FEF'=∠GEG',得出△GEG'≌△FEF',即可证出 的值,再根据HG′∥NG,同理可证
的值,再根据HG′∥NG,同理可证 ,得出EC=CH,得出△HCE是等腰直角三角形,在△HG'C中,求出CW的值,从而得出G′H 的值.
,得出EC=CH,得出△HCE是等腰直角三角形,在△HG'C中,求出CW的值,从而得出G′H 的值.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
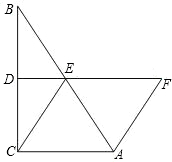 延长线上,且AF=CE.求证:四边形ACEF是菱形.
延长线上,且AF=CE.求证:四边形ACEF是菱形.查看答案和解析>>
科目:初中数学 来源: 题型:
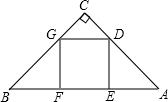 点G在边BC上.
点G在边BC上.| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com