
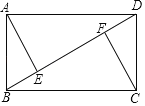
【题目】如图,在矩形ABCD中,点E,F在对角线BD上,BE=DF.请你判断:AE与CF的关系,并加以证明
【答案】AE与CF相等且平行;或相等且共线.理由详见解析
【解析】
AE与CF的关系分为数量关系和位置关系两种情况.由平行四边形的性质得出AD=CD,∠ABE=∠CDF,结合BE=DF可证明△ABE≌△CDF,根据全等三角形的性质可得出结论.
解:AE与CF相等且平行;或相等且共线.理由如下:
(1)数量关系:AE=CF.
∵四边形ABCD是矩形,
∴AB=CD,∠ABE=∠CDF,
在△ABE和△CDF中,
 ,
,
∴△ABE≌△CDF(SAS).
∴AE=CF.
(2)当点E与点F不在BD的中点时,AE∥FC.
∵△ABE≌△CDF,
∴∠AEB=∠CFD,
∴∠AED=∠CFB,
∴AE∥CF.
(3)当点E和点F在BD的中点时,AE与CF共线.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() 与
与![]() 轴交于点
轴交于点![]() 二次函数
二次函数![]() 的图象经过
的图象经过![]() 两点,且与
两点,且与![]() 轴的负半轴交于点
轴的负半轴交于点![]() .
.
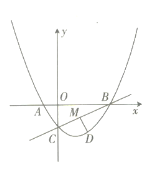
![]() 求二次函数的解析式及点
求二次函数的解析式及点![]() 的坐标.
的坐标.
![]() 点
点![]() 是线段
是线段![]() 上的一动点,动点
上的一动点,动点![]() 在直线
在直线![]() 下方的二次函数图象上.设点
下方的二次函数图象上.设点![]() 的横坐标为
的横坐标为![]() .过点
.过点![]() 作
作![]() 于点
于点![]() 求线段
求线段![]() 的长关于
的长关于![]() 的函数解析式,并求线段
的函数解析式,并求线段![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
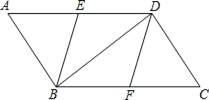
【题目】如图,在ABCD中,点E、F分别是AD、BC的中点,分别连接BE、DF、BD.
(1)求证:△AEB≌△CFD;
(2)若四边形EBFD是菱形,求∠ABD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
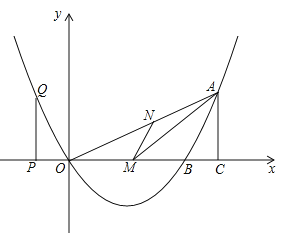
【题目】如图,已知二次函数的图象过点![]() .
.![]() ,与
,与![]() 轴交于另一点
轴交于另一点![]() ,且对称轴是直线
,且对称轴是直线![]() .
.
(1)求该二次函数的解析式;
(2)若![]() 是
是![]() 上的一点,作
上的一点,作![]() 交
交![]() 于
于![]() ,当
,当![]() 面积最大时,求
面积最大时,求![]() 的长;
的长;
(3)![]() 是
是![]() 轴上的点,过
轴上的点,过![]() 作
作![]() 轴与抛物线交于
轴与抛物线交于![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() ,当以
,当以![]() 为顶点的三角形与以
为顶点的三角形与以![]() 为顶点的三角形相似时,求
为顶点的三角形相似时,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
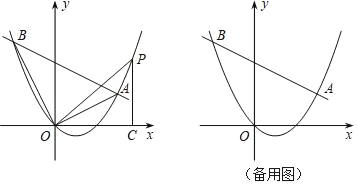
【题目】如图,在平面直角坐标系中,直线y=kx﹣4k+4与抛物线y=![]() x2﹣x交于A、B两点.
x2﹣x交于A、B两点.
(1)直线总经过定点,请直接写出该定点的坐标;
(2)点P在抛物线上,当k=﹣![]() 时,解决下列问题:
时,解决下列问题:
①在直线AB下方的抛物线上求点P,使得△PAB的面积等于20;
②连接OA,OB,OP,作PC⊥x轴于点C,若△POC和△ABO相似,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017江西省)如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售部为了调动销售员的积极性,决定实行目标管理,根据目标完成的情况对销售员进行适当的奖励.为了确定一个适当的月销售目标,该公司统计了销售部每位销售员在某月的销售额(单位:万元),并将结果绘制成如图所示的统计图.
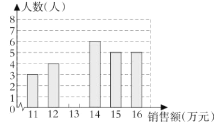
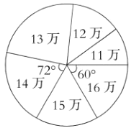
图1 图2
(1)补全如图1所示的统计图;
(2)月销售额在 万元的人数最多,该公司销售部人均月销售额是 万元;
(3)若想让一半左右的销售员都能达到销售目标,你认为月销售额定为多少合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=mx+n与双曲线y=![]() 相交于A(﹣1,2)、B(2,b)两点,与y轴相交于点C.
相交于A(﹣1,2)、B(2,b)两点,与y轴相交于点C.
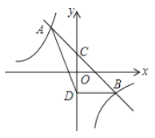
(1)求m,n的值;
(2)若点D与点C关于x轴对称,求△ABD的面积;
(3)在坐标轴上是否存在异于D点的点P,使得S△PAB=S△DAB?若存在,直接写出P点坐标;若不存在,说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com