
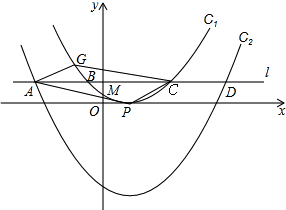
分析 (1)把(0,1)代入y=a(x-3)2求出a即可;
(2)先由轴对称得:点M是AC的中点,再根据平行四边形的对角线互相平分可知:PG也过点M,且点M也是PG的中点;
(3)作辅助线构建两直角三角形,证全等,得出点G的坐标,代入抛物线C1的解析式即可求出m的值;
(4)由对称性表示出点A的坐标,代入抛物线C2的解析式,求出h的值,写出解析式即可.
解答 解:(1)把(0,1)代入y=a(x-3)2得:1=a(0-3)2,
a=$\frac{1}{9}$;
(2)连接PG,
∵A,C两点关于y轴对称且AC交y轴于M,
∴M是AC的中点,
∵四边形APCG是平行四边形,
∴PG一定过点M,
∴点M为PG中点;
(3)抛物线C1:y=$\frac{1}{9}$(x-3)2,P(3,0),
当y=m2时,$\frac{1}{9}$(x-3)2=m2,
(x-3)2=9m2,
x-3=±3m,
x1=3+3m,x2=3-3m,
过G作GH⊥AC,垂足为H,
∵MG=MP,∠GMH=∠MPO,∠GHM=∠MOP=90°,
∴△GHM≌△MOP,
∴GH=MO=m2,HM=OP=3,
∴G(-3,2m2),
∵G在抛物线C1上,
∴2m2=$\frac{1}{9}$(-3-3)2,
2m2=4,
m=±$\sqrt{2}$,
∵m>0,
∴m=$\sqrt{2}$;
(4)M(0,2),C(3+3$\sqrt{2}$,2),
∵A,C两点关于y轴对称,
∴A(-3-3$\sqrt{2}$,2),
∵抛物线C2的解析式为:y=$\frac{1}{9}$(x-3)2-h且点A在抛物线C2上,
∴2=$\frac{1}{9}$(-3-3$\sqrt{2}$-3)2-h,
h=$\frac{1}{9}$(6+3$\sqrt{2}$)2-2,
h=$\frac{1}{9}$(54+36$\sqrt{2}$)-2=4+4$\sqrt{2}$,
∴抛物线C2的解析式为:y=$\frac{1}{9}$(x-3)2-4-4$\sqrt{2}$.
点评 本题是二次函数的综合题,考查了二次函数的顶点式及平移问题,还考查了平行四边形的性质和轴对称的性质;本题把函数和几何问题有机结合在一起,通过证两直角三角形全等得相等线段,表示出抛物线上点的坐标,利用抛物线的解析式这一等量关系列方程得出m和h的值,使问题得以解决.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:初中数学 来源: 题型:解答题
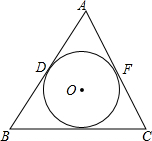 如图,⊙O内切于△ABC,切点分别为D、E、F
如图,⊙O内切于△ABC,切点分别为D、E、F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO、BO的中点.若AC+BD=24cm,EF的长为3cm,则△OAB的周长是( )
如图,?ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO、BO的中点.若AC+BD=24cm,EF的长为3cm,则△OAB的周长是( )| A. | 16cm | B. | 18cm | C. | 20cm | D. | 22cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
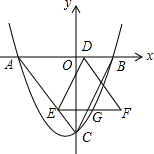 如图,抛物线y=ax2+bx-4经过A(-3,0)、B(2,0)两点,与y轴的交点为C,连接AC、BC,D为线段AB上的动点,DE∥BC交AC于E,A关于DE的对称点为F,连接DF、EF.
如图,抛物线y=ax2+bx-4经过A(-3,0)、B(2,0)两点,与y轴的交点为C,连接AC、BC,D为线段AB上的动点,DE∥BC交AC于E,A关于DE的对称点为F,连接DF、EF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com