
【题目】某车行经销的![]() 型自行车去年
型自行车去年![]() 月份销售总额为
月份销售总额为![]() 万元,今年由于改造升级每辆车售价比去年增加
万元,今年由于改造升级每辆车售价比去年增加![]() 元,今年
元,今年![]() 月份与去年同期相比,销售数量相同,销售总额增加
月份与去年同期相比,销售数量相同,销售总额增加![]() .
.
(1)求今年![]() 型车每辆售价多少元?
型车每辆售价多少元?
(2)该车行计划![]() 月份用不超过
月份用不超过![]() 万元的资金新进一批
万元的资金新进一批![]() 型车和
型车和![]() 型车共
型车共![]() 辆,应如何进货才能使这批车售完后获利最多?
辆,应如何进货才能使这批车售完后获利最多?
今年![]() 、
、![]() 两种型号车的进价和售价如下表:
两种型号车的进价和售价如下表:
|
| |
进价(元/辆) |
|
|
售价(元/辆) | 今年售价 |
|
【答案】(1)今年A型车每辆售价为1000元;(2)当购进A型车30辆、购进B型车20辆时,才能使这批车售完后获利最多.
【解析】
(1)设今年A型车每辆售价为x元,则去年A型车每辆售价为(x200)元,根据数量=总价÷单价,结合今年6月份与去年同期相比销售数量相同,即可得出关于x的分式方程,解之经检验后即可得出结论;
(2)设购进A型车m辆,则购进B型车(50m)辆,根据总价=单价×数量结合总费用不超过4.3万元,即可得出关于m的一元一次不等式,解之即可得出m的取值范围,再根据销售利润=单辆利润×购进数量即可得出销售利润关于m的函数关系式,利用一次函数的性质解决最值问题即可.
解:(1)设今年A型车每辆售价为x元,则去年A型车每辆售价为(x200)元,
根据题意得:![]() ,
,
解得:x=1000,
经检验,x=1000是原分式方程的解,
答:今年A型车每辆售价为1000元;
(2)设购进A型车m辆,则购进B型车(50m)辆,
根据题意得:800m+950(50m)≤43000,
解得:m≥30.
销售利润为:(1000800)m+(1200950)(50m)=50m+12500,
∵50<0,
∴当m=30时,销售利润最多,50-30=20(辆),
答:当购进A型车30辆、购进B型车20辆时,才能使这批车售完后获利最多.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的袋子里装有2个红球1个黄球,这3个小球除颜色不同外,其它都相同,贝贝同学摸出一个球后放回口袋再摸一个;莹莹同学一次摸2个球,两人分别记录下小球的颜色,关于两人摸到1个红球1个黄球和2个红球的概率的描述中,正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的个数有( )
①绝对值最小的有理数是0;②两个有理数比较大小,绝对值大的反而小;③用一个平面去截一个正方体,截面可能是六边形;④有理数分为正有理数和负有理数;⑤在数轴上,与表示3的点的距离等于4的点所表示的数为7;⑥当![]() 时,
时,![]() .
.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
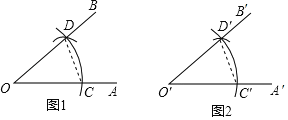
【题目】已知:∠AOB.
求作:∠A'O'B',使∠A'O′B'=∠AOB
(1)如图1,以点O为圆心,任意长为半径画弧,分别交OA,OB于点C、D;
(2)如图2,画一条射线O′A′,以点O′为圆心,OC长为半径间弧,交O′A′于点C′;
(3)以点C′为圆心,CD长为半径画弧,与第2步中所而的弧交于点D′;
(4)过点D′画射线O′B',则∠A'O'B'=∠AOB.
根据以上作图步骤,请你证明∠A'O'B′=∠AOB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(阅读理解)
点A、B、C为数轴上三点,如果点C在A、B之间且到A的距离是点C到B的距离3倍,那么我们就称点C是{A,B}的奇点.
例如,如图1,点A表示的数为﹣3,点B表示的数为1.表示0的点C到点A的距离是3,到点B的距离是1,那么点C是{A,B}的奇点;又如,表示﹣2的点D到点A的距离是1,到点B的距离是3,那么点D就不是{A,B}的奇点,但点D是{B,A}的奇点.
(知识运用)
如图2,M、N为数轴上两点,点M所表示的数为﹣3,点N所表示的数为5.
(1)数 所表示的点是{M,N}的奇点;数 所表示的点是{N,M}的奇点;
(2)如图3,A、B为数轴上两点,点A所表示的数为﹣50,点B所表示的数为30.现有一动点P从点B出发向左运动,当P点运动到数轴上的什么位置时,P、A和B中恰有一个点为其余两点的奇点?

查看答案和解析>>
科目:初中数学 来源: 题型:
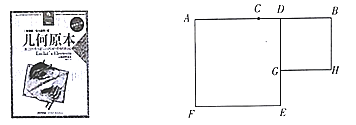
【题目】在《几何原本》中记载着这样的题目:如果同一条线段被两个分点先后分成相等和不相等的线段,以得到的各线段为边作正方形,那么不相等的两个正方形的面积之和等于原线段一半上的正方形与两个分点之间一段上正方形的面积之和的两倍.王老师带领学生在阅读的基础上画出的部分图形如图,已知线段![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 上任意一点(
上任意一点(![]() 不与
不与![]() 重合),分别以
重合),分别以![]() 和
和![]() 为边在
为边在![]() 的下方作正方形
的下方作正方形![]() 和正方形
和正方形![]() ,以
,以![]() 和
和![]() 为边在线段下方作正方形
为边在线段下方作正方形![]() 和正方形
和正方形![]() ,则正方形
,则正方形![]() 与正方形
与正方形![]() 的面积之和等于正方形
的面积之和等于正方形![]() 和正方形
和正方形![]() 面积之和的两倍.
面积之和的两倍.
(1)请你画出正方形![]() 和正方形
和正方形![]() (不必尺规作图);
(不必尺规作图);
(2)设![]() ,
,![]() ,根据题意写出关于
,根据题意写出关于![]() 的等式并证明.
的等式并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知![]() 的三个顶点坐标分别是
的三个顶点坐标分别是![]() ,
,![]() ,
,![]() .
.
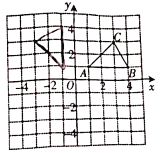
(1)将入![]() 向下平移
向下平移![]() 个单位后得到
个单位后得到![]() ,请画出
,请画出![]() ;
;
(2)将![]() 绕原点
绕原点![]() 逆时针旋转
逆时针旋转![]() 后得到
后得到![]() ,请画出
,请画出![]() ;
;
(3)判断以![]() 、
、![]() 、
、![]() 为顶点的三角形的形状.(无须说明理由)
为顶点的三角形的形状.(无须说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣![]() x2+bx+c的图象经过A(0,3),B(﹣4,﹣
x2+bx+c的图象经过A(0,3),B(﹣4,﹣![]() )两点.
)两点.
(1)求b,c的值.
(2)二次函数y=﹣![]() x2+bx+c的图象与x轴是否有公共点,求公共点的坐标;若没有,请说明情况.
x2+bx+c的图象与x轴是否有公共点,求公共点的坐标;若没有,请说明情况.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com