
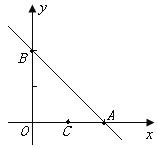
【题目】如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴交点分别为
轴交点分别为![]() 、
、![]() ,另一直线
,另一直线![]()
![]() 经过
经过![]() ,且把
,且把![]() 分成两部分.
分成两部分.
(1)若![]() 被分成的两部分面积相等,求
被分成的两部分面积相等,求![]() 和
和![]() 的值.
的值.
(2)若![]() 被分成的两部分面积之比为
被分成的两部分面积之比为![]() ,求
,求![]() 和
和![]() 的值.
的值.
【答案】(1)k=-2,b=2;(2)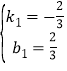 或
或![]()
【解析】
(1)△AOB被分成的两部分面积相等,那么被分成的两部分都应该是三角形AOB的面积的一半,那么直线y=kx+b(k≠0)必过B点,因此根据B,C两点的函数关系式可得出,直线的函数式.
(2)若△AOB被分成的两部分面积比为1:5,那么被分成的两部分中小三角形的面积就应该是大三角形面积的![]() ,已知了直线过C点,则小三角形的底边是大三角形的OA边的一半,故小三角形的高应该是OB的
,已知了直线过C点,则小三角形的底边是大三角形的OA边的一半,故小三角形的高应该是OB的![]() ,即直线经过的这点的纵坐标应该是
,即直线经过的这点的纵坐标应该是![]() .那么这点应该在y轴和AB上,可分这两种情况进行计算,运用待定系数法求函数的解析式.
.那么这点应该在y轴和AB上,可分这两种情况进行计算,运用待定系数法求函数的解析式.
(1)由题意知:直线y=kx+b(k≠0)必过C点,
∵C是OA的中点,
∴直线y=kx+b一定经过点B,C,如图(1)所示,
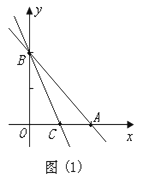
把B,C的坐标代入可得:
![]() ,
,
解得k=2,b=2;
(2)∵S△AOB=12×2×2=2,
∵△AOB被分成的两部分面积比为1:5,那么直线y=kx+b(k≠0)与y轴或AB交点的纵坐标就应该是:2×2×![]() =
=![]() ,
,
①当y=kx+b(k≠0)与直线y=x+2相交时,交点为D,如图(2)所示,
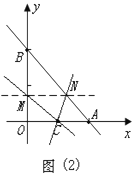
当y=![]() 时,直线y=x+2与y=kx+b(k≠0)的交点D的横坐标就应该是x+2=
时,直线y=x+2与y=kx+b(k≠0)的交点D的横坐标就应该是x+2=![]() ,
,
∴x=![]() ,
,
即交点D的坐标为(![]() ,
,![]() ),
),
又根据C点的坐标为(1,0),可得:
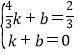
∴k=2,b=2,
②当y=kx+b(k≠0)与y轴相交时,交点为E,如图(3)所示,
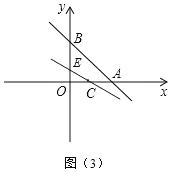
∴交点E的坐标就应该是(0,![]() ),又有C点的坐标(1,0),可得:
),又有C点的坐标(1,0),可得:
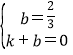
∴
k=![]() ,b=
,b=![]() ,
,
因此:k=2,b=2或k=![]() ,b=
,b=![]() .
.


 名题金卷系列答案
名题金卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,分别延长△ABC的边AB、AC到D、E,∠CBD与∠BCE的平分线相交于点P,爱动脑筋的小明在写作业的时发现如下规律:
(1)若∠A=60°,则∠P= °;
(2)若∠A=40°,则∠P= °;
(3)若∠A=100°,则∠P= °;
(4)请你用数学表达式归纳∠A与∠P的关系 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是矩形ABCD的一条对角线. 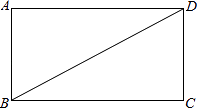
(1)作BD的垂直平分线EF,分别交AD、BC于点E、F,垂足为点O.(要求用尺规作图,保留作图痕迹,不要求写作法);
(2)求证:DE=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是矩形ABCD的一条对角线. 
(1)作BD的垂直平分线EF,分别交AD、BC于点E、F,垂足为点O.(要求用尺规作图,保留作图痕迹,不要求写作法);
(2)求证:DE=BF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形ABCD中,AB=10 cm,BC=8 cm.点P从点A出发,沿A→B→C→D的路线运动,到点D停止;点Q从点D出发,沿D→C→B→A的路线运动,到点A停止.若点P、点Q同时出发,点P的速度为每秒1 cm,点Q的速度为每秒2 cm,a秒时,点P、点Q同时改变速度,点P的速度变为每秒b cm,点Q的速度变为每秒d cm.图②是点P出发x秒后△APD的面积S1(cm2)与时间x(秒)的函数关系图象;图③是点Q出发x秒后△AQD的面积S2(cm2)与时间x(秒)的函数关系图象.
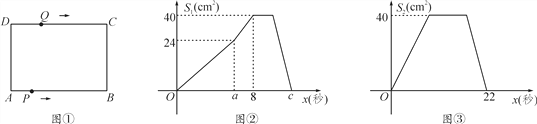
(1)参照图②,求a、 b及图②中c的值;
(2)求d的值;
(3)设点P离开点A的路程为y1(cm),点Q到点A还需要走的路程为y2(cm),请分别写出改变速度后,y1、y2与出发后的运动时间x(秒)的函数关系式,并求出点P、点Q相遇时x的值;
(4)当点Q出发__ __秒时,点Q的运动路程为25 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题8分)某校为了解学生体质情况,从各年级学生中随机抽取部分学生进行体能测试.
每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级.统计员在将测试数据绘制 成图表时发现,优秀漏统计4人,良好漏统计6人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题: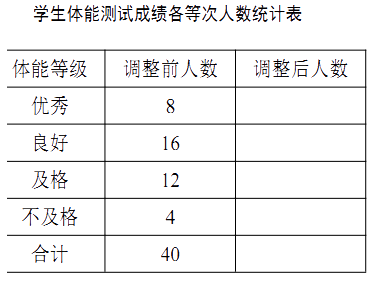
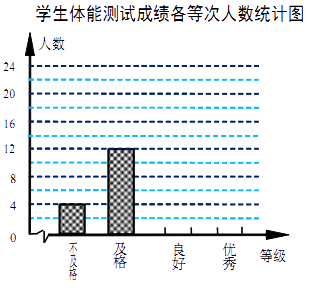
(1)填写统计表.
(2)根据调整后数据,补全条形统计图.
(3)若该校共有学生1500人,请你估算出该校体能测试等级为“优秀”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)数轴上有两点 A、B 对应的数为 a、b,AB表示这两个点间的距离,这两个点的中点所对应的数为![]() .
.
已知数轴上有三点 A、B、C,对应的数分别为 a、b、c,a、b、c 满足以下两个条件:①![]() ② a-b+c=0.
② a-b+c=0.
(1)求出 a、b、c 的值;
(2)若数轴上有一点 P,PA=3PB,求出满足条件的P点所对应的数;
(3)点A以每秒钟2个单位长度的速度向左运动,点B以每秒钟4个单位长度的速度向右运动,点C以每秒钟6个单位长度的速度向右运动.它们同时出发,M为AB 的中点,N为BC的中点,Q为AC的中点,O为原点,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
为了响应“十三五”规划中提出的绿色环保的倡议,某校文印室提出了每个人都践行“双面打印,节约用纸”.已知打印一份资料,如果用A4厚型纸单面打印,总质量为400克,将其全部改成双面打印,用纸将减少一半;如果用A4薄型纸双面打印,这份资料的总质量为160克,已知每页薄型纸比厚型纸轻0.8克,求A4薄型纸每页的质量.(墨的质量忽略不计)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com