

分析 (1)根据等边三角形的性质得出AC=AO,AE=AD,∠OAC=∠EAD=60°,求出∠CAE=∠DAO,根据SAS证△CAE≌△OAD,即可得出结论;
(2)由全等三角形的性质得出∠ACE=∠AOD=90°,求出∠CAE=50°,即可得出∠AEC的度数.
(3)根据等边三角形的性质得出OA=AC,CP=CM,∠OCA=∠MCP=60°,求出∠OCP=∠ACM,根据SAS推出△OCP≌△ACM,推出∠COA=∠CAM=60°,求出∠OAN=∠MAP=60°,即可得出结果.
解答 (1)证明:如图所示: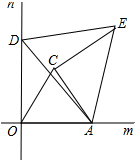
∵△OAC和△ADE是等边三角形,
∴AC=AO,AE=AD,∠OAC=∠DAE=60°
∴∠CAE=∠DAO=60○-∠CAD,
在△CAE和△OAD中,$\left\{\begin{array}{l}{AC=AO}&{\;}\\{∠CAE=∠OAD}&{\;}\\{AE=AD}&{\;}\end{array}\right.$,
∴△CAE≌△OAD(SAS),
∴CE=OD;
(2)解:由(1)得:△CAE≌△OAD,
∴∠ACE=∠AOD=90°,
∵∠DAC=10°,∠DAE=60°,
∴∠CAE=60°-10°=50°,
∴∠AEC=180°-90°-50°=40°.
(3)解:∠ANO的值不变化,其度数为30°
理由是:∵△AOC和△CPM是等边三角形,
∴OA=AC,CP=CM,∠OCA=∠MCP=60°,
∴∠OCP=∠ACM,
在△OCP和△ACM中,$\left\{\begin{array}{l}{OC=AC}&{\;}\\{∠OCP=∠ACM}&{\;}\\{CP=CM}&{\;}\end{array}\right.$,
∴△OCP≌△ACM(SAS),
∴∠COA=∠CAM=60°,
∴∠MAP=180°-60°-60°=60°,
∴∠OAN=∠MAP=60°,
∵∠AON=90°,
∴∠ANO=90°-60°=30°.
点评 本题是三角形综合题目,考查了等边三角形性质,全等三角形的性质和判定的应用;本题综合性强,难度适中,熟练掌握等边三角形的性质,证明三角形全等是解决问题的关键.


 星级口算天天练系列答案
星级口算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图在8×8的正方形网格中,△ABC的每个顶点都在格点(每个小正方形的顶点)上,把△ABC向右平移4个单位,在向上平移1个单位得△A1B1C1.
已知:如图在8×8的正方形网格中,△ABC的每个顶点都在格点(每个小正方形的顶点)上,把△ABC向右平移4个单位,在向上平移1个单位得△A1B1C1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1>y2>y3 | B. | y3>y1>y2 | C. | y3>y2>y1 | D. | y2>y1>y3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
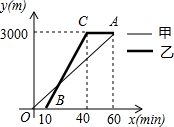 甲、乙两人从学校沿同一路线到距学校3000m的图书馆看书,甲先出发,他们距学校的路程y(m)与甲的行走时间x(min)之间的函数图象如图所示,根据图象解答下列问题:
甲、乙两人从学校沿同一路线到距学校3000m的图书馆看书,甲先出发,他们距学校的路程y(m)与甲的行走时间x(min)之间的函数图象如图所示,根据图象解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com