
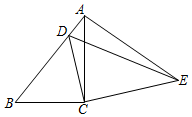
 如图,在△ABC中,∠ACB=90°,AB=18,cosB=$\frac{2}{3}$,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )
如图,在△ABC中,∠ACB=90°,AB=18,cosB=$\frac{2}{3}$,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E处,则线段AE的长为( )| A. | 6$\sqrt{5}$ | B. | 7$\sqrt{5}$ | C. | 8$\sqrt{5}$ | D. | 9$\sqrt{5}$ |
分析 先解直角△ABC,得出BC和AC的长.再根据旋转的性质得出BC=DC,AC=EC,∠BCD=∠ACE,利用等边对等角以及三角形内角和定理得出∠B=∠CAE.作CM⊥BD于M,作CN⊥AE于N,则∠BCM=$\frac{1}{2}$∠BCD,∠ACN=$\frac{1}{2}$∠ACE,∠BCM=∠ACN.解直角△ANC求出AN=AC•cos∠CAN,根据等腰三角形三线合一的性质得出AE=2AN,从而求解.
解答 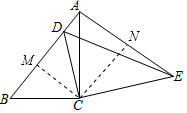 解:∵在△ABC中,∠ACB=90°,AB=9,cosB=$\frac{2}{3}$,
解:∵在△ABC中,∠ACB=90°,AB=9,cosB=$\frac{2}{3}$,
∴BC=AB•cosB=18×$\frac{2}{3}$=12,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=6$\sqrt{5}$.
∵把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,
∴△ABC≌△EDC,BC=DC=12,AC=EC=6$\sqrt{5}$,∠BCD=∠ACE,
∴∠B=∠CAE.
作CM⊥BD于M,作CN⊥AE于N,则∠BCM=$\frac{1}{2}$∠BCD,∠ACN=$\frac{1}{2}$∠ACE,
∴∠BCM=∠ACN.
∵在△ANC中,∠ANC=90°,AC=6$\sqrt{5}$,cos∠CAN=cosB=$\frac{2}{3}$,
∴AN=AC•cos∠CAN=6$\sqrt{5}$×$\frac{2}{3}$=4$\sqrt{5}$,
∴AE=2AN=8$\sqrt{5}$.
故选C.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了解直角三角形以及等腰三角形的性质.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
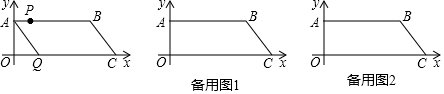
 如图,∠AOB内有一点P.
如图,∠AOB内有一点P.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=2,b=3 | B. | a=-2,b=-3 | C. | a=-2,b=3 | D. | a=2,b=-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{18}$ | B. | $\sqrt{\frac{2}{3}}$ | C. | $\root{3}{12}$ | D. | -2$\sqrt{27}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,将正六边形ABCDEF放入平面直角坐标系后,若点A、B、E的坐标分别为(a,b)、(3,1)、(-a,b),则点D的坐标为( )
如图,将正六边形ABCDEF放入平面直角坐标系后,若点A、B、E的坐标分别为(a,b)、(3,1)、(-a,b),则点D的坐标为( )| A. | (1,3) | B. | (3,-1) | C. | (-1,-3) | D. | (-3,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形ABCD内接于⊙O,AB=AD,连接BD,若∠C=120°,AB=2,则△ABD的周长是( )
如图,四边形ABCD内接于⊙O,AB=AD,连接BD,若∠C=120°,AB=2,则△ABD的周长是( )| A. | 3$\sqrt{3}$ | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com