
【题目】如图把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′位置,若∠EFB=60°,则∠AED′=( ) 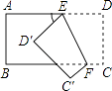
A.50°
B.55°
C.60°
D.65°
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:初中数学 来源: 题型:
【题目】2008北京奥运会主会场“鸟巢”的座席数是91 000个,这个数用科学记数法表示为( )
A.0.91×105
B.9.1×104
C.91×103
D.9.1×103
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1:已知△ABC中,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE、CD,请你完成图形(尺规作图,不写作法.但要保留作图痕迹).
(2)如图2,已知△ABC中,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE、CD,判断BE与CD有什么数量关系,并加以证明.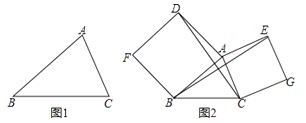
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市出租车收费标准是:起步价8元,当路程超过2km时,每1km收费1.8元,如果某出租车行驶x(x>2km),则司机应收费(单位:元)( )
A. 8+1.8(x﹣2)B. 8+1.8xC. 8﹣1.8xD. 8﹣1.8(x﹣2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y= ![]() x与一次函数y=﹣x+7的图象交于点A.
x与一次函数y=﹣x+7的图象交于点A. 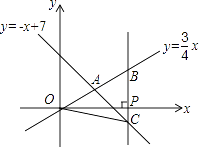
(1)求点A的坐标;
(2)设x轴上有一点P(a,0),过点P作x轴的垂线(垂线位于点A的右侧),分别交y= ![]() x和y=﹣x+7的图象于点B,C,连接OC.若BC=
x和y=﹣x+7的图象于点B,C,连接OC.若BC= ![]() OA,求△OBC的面积.
OA,求△OBC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形OABC是边长为4的正方形,分别以OA,OC所在的直线为x轴、y轴,建立如图1所示的平面直角坐标系,直线l经过A,C两点.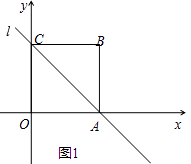
(1)写出点A,点C坐标并求直线l的函数表达式;
(2)若P是直线l上的一点,当△OPA的面积是5时,请求出点P的坐标;
(3)如图2,点D(3,﹣1),E是直线l上的一个动点,求出使|BE﹣DE|取得最大值时点E的坐标和最大值(不需要证明).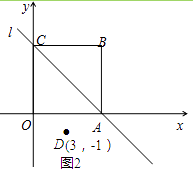
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com