
分析 (1)利用待定系数法即可解决.
(2)分两种情形列方程解决问题:①如图2中,当E在P右边时,作EM⊥x轴于M.设E(m,2)则F(1,2m),②如图3中,当E在P左边时,作EM⊥x轴于M.设E(m,2)则F(1,2m),
(3)分四种情形①如图4中,当E在P右边时,∠FEG=90°,EF=EG,设E(m,2),则F(1,2m),②如图5中,当E在P右边时,∠GFE=90°,FG=FE,作FM⊥y轴于M.设E(m,2),则F(1,2m),③如图6中,当E在P左边时,∠FEG=90°,EG=EF.设E(m,2),则F(1,2m),④如图7中,当E在P左边时,∠EFG=90°,EF=FG,作GM⊥PA于M.设E(m,2),则F(1,2m),利用全等三角形的性质,列出方程即可解决问题.
解答 解:(1)如图1中,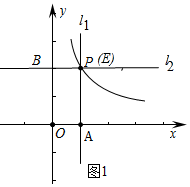
由题意P(1,2),把P(1,2)代入y=$\frac{k}{x}$得到,k=2,
∴k的值为2.
(2)①如图2中,当E在P右边时,作EM⊥x轴于M.设E(m,2)则F(1,2m),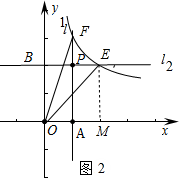
∵S△OEF=S△AOF+S梯形AMEF-S△OEM,S△AOF=S△EOM,
∴S△OEF=S梯形AMEF,
∵S△EOF=2S△PEF,
∴$\frac{2+2m}{2}$•(m-1)=2×$\frac{1}{2}$×(m-1)(2m-2),
∴m=3,
此时E(3,2)
②如图3中,当E在P左边时,作EM⊥x轴于M.设E(m,2)则F(1,2m),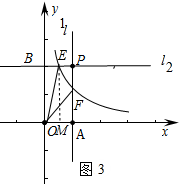
同理可得,$\frac{2+2m}{2}$×(1-m)=2×$\frac{1}{2}$(1-m)×(2-2m),
∴m=$\frac{1}{3}$,
此时E($\frac{1}{3}$,2)
综上所述,当E(3,2)或($\frac{1}{3}$,2)时,△OEF的面积为△PEF面积的2倍.
(3)如图4中,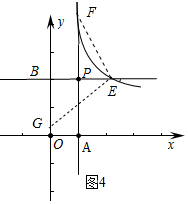
①当E在P右边时,∠FEG=90°,EF=EG,设E(m,2),则F(1,2m),
∵∠EPF=∠EBG,EF=EG,∠FEP=∠BEG,
∴△FEP≌△EGB,
∴PF=BE,BG=PE,
∴m=2m-2,
∴m=2,
∴BG=PE=1,
∴G(0,1).
②如图5中,当E在P右边时,∠GFE=90°,FG=FE,作FM⊥y轴于M.设E(m,2),则F(1,2m),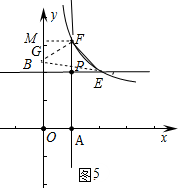
由△FPE≌△FMG,得到FM=PF,MG=PE,
∴2m-2=1,
∴m=$\frac{3}{2}$,
∴PE=MG=$\frac{1}{2}$,BG=$\frac{1}{2}$,
∴G(0,$\frac{5}{2}$).
③如图6中,当E在P左边时,∠FEG=90°,EG=EF.设E(m,2),则F(1,2m),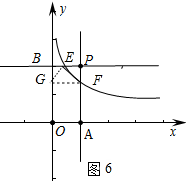
由△EFP≌△GEB,得到,EB-PF,BG=PE,
∴m=2-2m,
∴m=$\frac{1}{3}$,
∴BG=PE=$\frac{2}{3}$,OG=$\frac{4}{3}$,
∴G(0,$\frac{4}{3}$).
④如图7中,当E在P左边时,∠EFG=90°,EF=FG,作GM⊥PA于M.设E(m,2),则F(1,2m),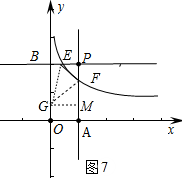
由△EFP≌△FGM得到PE=FM,PF=GM,
∴2-2m=1,
∴m=$\frac{1}{2}$,
∴BG=PF+FM=$\frac{3}{2}$,
∴OG=$\frac{1}{2}$,
∴G(0,$\frac{1}{2}$),
综上所述,满足条件的点G左边为(0,1)或(0,$\frac{5}{2}$) 或(0,$\frac{4}{3}$)或(0,$\frac{1}{2}$).
点评 本题考查反比例函数综合题、待定系数法、全等三角形的判定和性质、三角形的面积等知识,解题的关键是学会利用分割法求三角形的面积,学会用分类讨论的思想思考问题,学会用方程的思想思考问题,属于中考压轴题.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:解答题
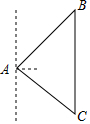 随着南海局势的升级,中国政府决定在黄岩岛填海造陆,修建机场,设立雷达塔.某日,在雷达塔A处侦测到东北方向上的点B处有一艘菲律宾渔船进入我侦测区域,且以30海里/时的速度往正南方向航行,我方与其进行多次无线电沟通无果后,这艘渔船行驶了1小时10分到达点A南偏东53°方向的C处,与此同时我方立即通知(通知时间忽略不计)与A、C在一条直线上的中国海警船往正西方向对该渔船进行侦测拦截,其中海警船位于与A相距100海里的D处.
随着南海局势的升级,中国政府决定在黄岩岛填海造陆,修建机场,设立雷达塔.某日,在雷达塔A处侦测到东北方向上的点B处有一艘菲律宾渔船进入我侦测区域,且以30海里/时的速度往正南方向航行,我方与其进行多次无线电沟通无果后,这艘渔船行驶了1小时10分到达点A南偏东53°方向的C处,与此同时我方立即通知(通知时间忽略不计)与A、C在一条直线上的中国海警船往正西方向对该渔船进行侦测拦截,其中海警船位于与A相距100海里的D处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
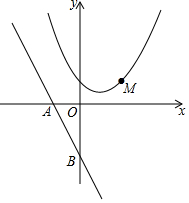 直线y=-$\frac{4}{3}$x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).
直线y=-$\frac{4}{3}$x-4与x轴交于点A,与y轴交于点B,抛物线y=x2-4x+5上的一点M(3,2).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\root{3}{16}$ | B. | $\sqrt{a}$ | C. | $\sqrt{-{a}^{2}-1}$ | D. | $\sqrt{{a}^{2}+2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com