[题目]用一个平面去截球.截面是 . 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】用一个平面去截球，截面是________.

【答案】圆

【解析】

截面：用一个平面去截一个几何体，截出的面叫做截面．依此即可求解．

用一个平面去截一个球，截面是圆.

故答案为：圆.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】①如图1,AB∥CD,则∠A +∠E +∠C=180°；②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E－∠1=180° ； ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )

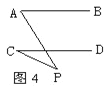
A. 、1个 B. 2个 C. 3个 D. 4个

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】已知，如图，B，C两点把线段AD分成2：5：3三部分，M为AD的中点，BM=6cm，求CM和AD的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】对于平面直角坐标系xOy中的点P（a，b），若点P′的坐标为（a＋kb，ka＋b）（其中k为常数，且k≠0），则称点P′为点P的“k属派生点”．

例如：P（1，4）的“2属派生点”为P′（1＋2×4，2×1＋4），即P′（9，6）．

（1）点P（－1，6）的“2属派生点”P′的坐标为_____________；

（2）若点P的“3属派生点”P′的坐标为（6，2），则点P的坐标___________；

（3）若点P在x轴的正半轴上，点P的“k属派生点”为P′点，且线段PP′的长度为线段OP长度的2倍，求k的值．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，已知∠DAB+∠D=180°，AC平分∠DAB，且∠CAD=25°，∠B=95°．求：∠DCE和∠DCA的度数．

请将以下解答补充完整，

解：因为∠DAB+∠D=180°

所以DC∥AB__________

所以∠DCE=∠B__________

又因为∠B=95°，

所以∠DCE=________°；

因为AC平分∠DAB，∠CAD=25°，根据角平分线定义，

所以∠CAB=________=________°，

因为DC∥AB

所以∠DCA=∠CAB，__________

所以∠DCA=________°．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某企业今年8月的产值为a万元， 9月份比8月份增加了10%，10月份比9月份增加了15%，则10月份的产值是（）

A.a(1 10%)(1 15%)万元B.(a 10%)(a 15%)万元

C.a(1 90%)(1 85%)万元D.a(1 10% 15%)万元

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】阅读下面材料：随着人们认识的不断深入，毕达哥拉斯学派逐渐承认不是有理数，并给出了证明．假设是有理数，那么存在两个互质的正整数p，q，使得，于是，两边平方得p2=2q2 ．因为2q2是偶数，所以p2是偶数，而只有偶数的平方才是偶数，所以p也是偶数．因此可设p=2s，代入上式，得4s2=2q2 ，即q2=2s2 ，所以q也是偶数，这样，p和q都是偶数，不互质，这与假设p，q互质矛盾，这个矛盾说明，不能写成分数的形式，即不是有理数．请你有类似的方法，证明不是有理数．