
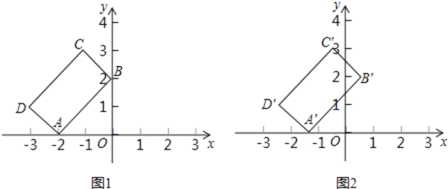
【题目】在平面直角坐标系xOy中,矩形ABCD的位置如图1所示,点A的坐标为(-2,0),点B的坐标为(0,2),点D的坐标为(-3,1).矩形ABCD以每秒1个单位长度的速度沿x轴正方向运动,设运动时间为x(0≤x≤3)秒,第一象限内的图形面积为y,则下列图象中表示y与x的函数关系的图象大致是
A. 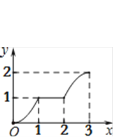 B.
B. 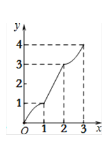 C.
C. 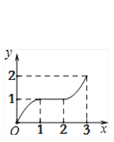 D.
D. 
【答案】D
【解析】根据点A、B、D的坐标求出OA=OB=2,△AOB是等腰直角三角形,AD= ![]() ,AB=
,AB= ![]() ,再根据矩形的性质得出AD=BC=
,再根据矩形的性质得出AD=BC=![]() ,AB=CD=
,AB=CD=![]() ,∠DAB=∠ABC=∠C=∠D=90°,当矩形从第二象限移至第一象限时应分三种情况进行讨论:①当0≤x≤1时,矩形ABCD落在第一象限内的图形是三角形FB′G,利用三角形的面积公式表示出y与x的函数关系式,②当1<x≤2时,矩形ABCD落在第一象限内的图形是梯形FB′C′G,利用梯形的面积公式表示出y与x的函数关系式,③当2<x≤3时,矩形ABCD落在第一象限内的图形是五边形FA′B′C′G,利用矩形的面积减去三角形的面积,列式整理得到y与x的函数关系式,从而判断出函数图象.
,∠DAB=∠ABC=∠C=∠D=90°,当矩形从第二象限移至第一象限时应分三种情况进行讨论:①当0≤x≤1时,矩形ABCD落在第一象限内的图形是三角形FB′G,利用三角形的面积公式表示出y与x的函数关系式,②当1<x≤2时,矩形ABCD落在第一象限内的图形是梯形FB′C′G,利用梯形的面积公式表示出y与x的函数关系式,③当2<x≤3时,矩形ABCD落在第一象限内的图形是五边形FA′B′C′G,利用矩形的面积减去三角形的面积,列式整理得到y与x的函数关系式,从而判断出函数图象.
如图1,∵点A的坐标为(﹣2,0),点B的坐标为(0,2),点D的坐标为(﹣3,1),
∴OA=OB=2,△AOB是等腰直角三角形,AD=![]() =
=![]() ,
,
∴AB=2![]() ,
,
∵四边形ABCD是矩形,
∴AD=BC=![]() ,AB=CD=2
,AB=CD=2![]() ,∠DAB=∠ABC=∠C=∠D=90°.
,∠DAB=∠ABC=∠C=∠D=90°.
分三种情况:




当0≤x≤1时如图2所示,矩形ABCD落在第一象限内的图形是等腰直角△FB′G,
∴FG=2x,
∴y=![]() 2x
2x![]() x =
x =![]()
当1<x≤2时,矩形ABCD落在第一象限内的图形是梯形FB′CG,如图3.
∵OA′=2﹣x,△A′OF是等腰直角三角形,
∴A′F= OA′= (2﹣x),
∴FB′=A′B′﹣A′F=![]() ﹣
﹣![]() =
= ![]() ,
,
C′G=![]() =
= ![]()
∴y= ![]() (C′G+B′F)B′C′=
(C′G+B′F)B′C′= ![]() (
( ![]() +
+ ![]() )×
)×![]() =2x﹣1;
=2x﹣1;
当2<x≤3时,矩形ABCD落在第一象限内的图形是五边形FA′B′CG,如图4.
∵FG=2(3-x)=6-2x,△D′FG是等腰直角三角形,
∴△D′FG的面积是![]() (6-2x)(3-x)=
(6-2x)(3-x)=![]() ,
,
∴y=4-(![]() )=
)=![]() ﹣x2+6x﹣5.
﹣x2+6x﹣5.
故D选项正确.


科目:初中数学 来源: 题型:
【题目】阅读下列材料,回答提出的问题.
我们知道:一个数![]() 的绝对值可以表示成
的绝对值可以表示成![]() ,它是一个非负数,在数轴上,
,它是一个非负数,在数轴上,![]() 表示
表示![]() 这个数在数轴上所对应的点到原点的距离(距离,当然不可能是负数),这正是绝对值的几何意义,比如说
这个数在数轴上所对应的点到原点的距离(距离,当然不可能是负数),这正是绝对值的几何意义,比如说![]() 表示2这个数在数轴上所对应的点到原点的距离,它是2,所以说
表示2这个数在数轴上所对应的点到原点的距离,它是2,所以说![]() 表示
表示![]() 这个数在数轴上所对应的点到原点的距离,它也是2,所以说
这个数在数轴上所对应的点到原点的距离,它也是2,所以说![]() ,严格来说,在数轴上,一个数
,严格来说,在数轴上,一个数![]() 在数轴上所对应的点到原点(原点对应的数为0)的距离应该表示为
在数轴上所对应的点到原点(原点对应的数为0)的距离应该表示为![]() ,但平时我们都写成
,但平时我们都写成![]() ,原因你明白.
,原因你明白.
(1)若给定![]() ,要找这样的x,请按照上面材料中的说法,解释它的几何意义并找出对应的
,要找这样的x,请按照上面材料中的说法,解释它的几何意义并找出对应的![]() ;
;
(2)实际上,对于数轴上任意两个数![]() 之间的距离我们也可以表示为
之间的距离我们也可以表示为![]() ,反过来,
,反过来,![]() 这个绝对值的几何意义就是:数轴上表示
这个绝对值的几何意义就是:数轴上表示![]() 与
与![]() 这两个数的点之间的距离,你能结合上面的叙述,解释
这两个数的点之间的距离,你能结合上面的叙述,解释![]() 的几何意义吗?请按你的理解说明:
的几何意义吗?请按你的理解说明:![]() 呢,如果能解释这个,你了不起;
呢,如果能解释这个,你了不起;
(3)若![]() ,请直接写出
,请直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有颜色不同的黑、白两种球共40个,小颖做摸球试验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是“摸到白色球”的频率折线统计图.
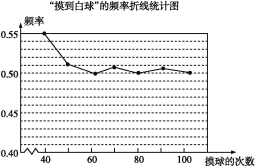
(1)请估计:当n足够大时,摸到白球的频率将会稳定在 (精确到0.01),假如你摸一次,你摸到白球的概率为 ;
(2)试估算盒子里白、黑两种颜色的球各有多少个?
(3)在(2)条件下如果要使摸到白球的概率为![]() ,需要往盒子里再放入多少个白球?
,需要往盒子里再放入多少个白球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,阶梯图的每个台阶上都标着一个数, 从下到上的第![]() 个至第
个至第![]() 个台阶上依次标着
个台阶上依次标着![]() ,且任意相邻四个台阶上的数的和都相等.
,且任意相邻四个台阶上的数的和都相等.

![]() 求前
求前![]() 个台阶上的数的和;
个台阶上的数的和;
![]() 求第
求第![]() 个台阶上的数x的值;
个台阶上的数x的值;
![]() 从下到上前
从下到上前![]() 为奇数)个台阶上的数的和能否为
为奇数)个台阶上的数的和能否为![]() ?若能,求出
?若能,求出![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:
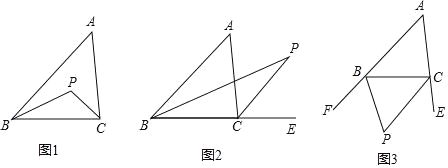
(1)如图1,在△ABC中,BP平分∠ABC,CP平分∠ACB.求证:∠P=90°+![]() ∠A.
∠A.
(2)如图2,在△ABC中,BP平分∠ABC,CP平分外角∠ACE.猜想∠P和∠A有何数量关系,并证明你的结论.
(3)如图3,BP平分∠CBF,CP平分∠BCE.猜想∠P和∠A有何数量关系,请直接写出结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在AB上,点E在AC上,BE、CD相交于点O.
(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了《展开与折叠》这一课后,明白了很多几何体都能展开成平面图形.于是他在家用剪刀展开了一个长方体纸盒,可是一不小心多剪了一条棱,把纸盒剪成了两部分,即图中的①和②.根据你所学的知识,回答下列问题:

(1)小明总共剪开了_______条棱.
(2)现在小明想将剪断的②重新粘贴到①上去,而且经过折叠以后,仍然可以还原成一个长方体纸盒,你认为他应该将剪断的纸条粘贴到①中的什么位置?请你帮助小明在①上补全.
(3)小明说:他所剪的所有棱中,最长的一条棱是最短的一条棱的5倍.现在已知这个长方体纸盒的底面是一个正方形,并且这个长方体纸盒所有棱长的和是880cm,求这个长方体纸盒的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在两条垂直相交的道路上,一辆自行车和一辆摩托车相遇后又分别向北向东驶去,若自行车与摩托车每秒分别行驶![]() 米、
米、![]() 米,则
米,则![]() 秒后两车相距( )米.
秒后两车相距( )米.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(![]() ),两个不全等的等腰直角三角形
),两个不全等的等腰直角三角形![]() 和
和![]() 叠放在一起,并且有公共的直角顶点
叠放在一起,并且有公共的直角顶点![]() .
.
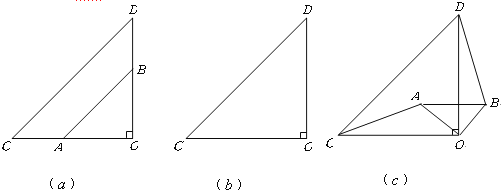
(1)将图(![]() )中的
)中的![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 角,在图(
角,在图(![]() )中作出旋转后的
)中作出旋转后的![]() (保留作图痕迹,不写作法,不证明).
(保留作图痕迹,不写作法,不证明).
(2)在图(![]() )中,你发现线段
)中,你发现线段![]() ,
,![]() 的数量关系是 ,直线
的数量关系是 ,直线![]() ,
,![]() 相交成 度角.
相交成 度角.
(3)将图(![]() )中的
)中的![]() 绕点
绕点![]() 顺时针旋转一个锐角,得到图(
顺时针旋转一个锐角,得到图(![]() ),这时(2)中的两个结论是否成立?作出判断并说明理由.若
),这时(2)中的两个结论是否成立?作出判断并说明理由.若![]() 绕点
绕点![]() 继续旋转更大的角时,结论仍然成立吗?作出判断,不必说明理由.
继续旋转更大的角时,结论仍然成立吗?作出判断,不必说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com