

分析 (1)根据正方形的性质、等边三角形的性质以及全等三角形的判定定理证明△BAE≌△ADF,根据全等三角形的性质进行证明;
(2)根据边边边定理、边角边定理证明三角形全等,根据全等三角形的性质解答;
(3)与(2)的证明方法相似,证明即可.
解答 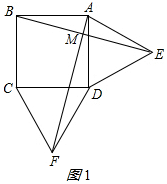 解:(1)AF=BE;AF⊥BE.理由如下:如图1所示:
解:(1)AF=BE;AF⊥BE.理由如下:如图1所示:
∵四边形ABCD是正方形,
∴∠BAD=∠ADC=90°,AB=AD=CD,
∵△ADE和△DCF是等边三角形,
∴∠DAE=∠CDF=60°,AE=AD,DF=CD,
∴AE=DF,∠BAE=∠ADF=150°,
在△BAE和△ADF中,$\left\{\begin{array}{l}{AB=AD}&{\;}\\{∠BAE=∠ADF}&{\;}\\{AE=DF}&{\;}\end{array}\right.$,
∴△BAE≌△ADF(SAS),
∴AF=BE,∠ABE=∠DAF.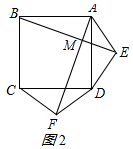
∵∠DAF+∠BAF=90°,
∴∠ABE+∠BAF=90°,
∴∠AMB=90°,
∴AF⊥BE;
(2)第(1)问中的结论仍然成立,其理由如下:如图2所示:
在正方形ABCD中,∠BAD=∠ADC=90°,AB=AD=CD.
∵EA=ED=FD=FC,
在△AED和△DFC中,$\left\{\begin{array}{l}{AE=DF}&{\;}\\{AD=DC}&{\;}\\{DE=CF}&{\;}\end{array}\right.$,
∴△AED≌△DFC(SSS),
∴∠EAD=∠FDC.
∴∠BAD+∠EAD=∠ADC+∠FDC.
即∠BAE=∠ADF.
在△BAE和△ADF中,$\left\{\begin{array}{l}{BA=AD}&{\;}\\{∠BAE=∠ADF}&{\;}\\{AE=DF}&{\;}\end{array}\right.$,
∴△BAE≌△ADF(SAS)
∴AF=BE,
∴∠ABE=∠DAF.
∵∠DAF+∠BAF=90°,
∴∠ABE+∠BAF=90°,
∴∠AMB=90°,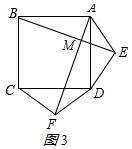
∴AF⊥BE.
(3)所画图形如图3,第(1)问的结论成立,理由如下:
在△AED和△DFC中,$\left\{\begin{array}{l}{AE=DF}&{\;}\\{AD=DC}&{\;}\\{DE=CF}&{\;}\end{array}\right.$,
∴△AED≌△DFC(SSS),
∴∠EAD=∠FDC.
∴∠BAD+∠EAD=∠ADC+∠FDC.即∠BAE=∠ADF.
在△BAE和△ADF中,$\left\{\begin{array}{l}{BA=AD}&{\;}\\{∠BAE=∠ADF}&{\;}\\{AE=DF}&{\;}\end{array}\right.$,
∴△BAE≌△ADF(SAS),
∴AF=BE,
∴∠ABE=∠DAF.
∵∠DAF+∠BAF=90°,
∴∠ABE+∠BAF=90°,
∴∠AMB=90°,
∴AF⊥BE.
点评 本题是四边形综合题目,考查的是正方形的性质、全等三角形的判定和性质、直角三角形的性质、等边三角形的性质、等腰三角形的性质等知识;本题综合性强,有一定难度,证明三角形全等是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 队别 | 平均分 | 众数 | 中位数 | 方差 | 合格率 | 优秀率 |
| 七年级 | 6.7 | a | m | 3.41 | 90% | 20% |
| 八年级 | 7.1 | p | q | 1.69 | 80% | 10% |
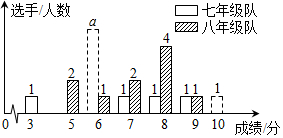
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,将四边形ABCD的对角线BD向两个方向延长,分别至点E和点F,且使BE=DF,若AE∥CF且AE=CF.
如图,将四边形ABCD的对角线BD向两个方向延长,分别至点E和点F,且使BE=DF,若AE∥CF且AE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com