
 如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,下面结论:
如图,已知平行四边形ABCD中,∠DBC=45°,DE⊥BC于E,BF⊥CD于F,下面结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①根据勾股定理和题目中的信息可以说明结论是否成立;
②根据平行四边形的性质和直角三角形的性质,可以说明结论是否成立;
③根据三角形的全等和平行四边形的性质可以说明结论是否正确;
④根据勾股定理、三角形的全等,灵活转化可以说明结论是否正确.
解答 解:∵∠DBC=45°,DE⊥BC于E,
∴∠DBE=∠BDE=45°,∠BED=90°,
∴BE=DE,
∴BD=$\sqrt{B{E}^{2}+D{E}^{2}}=\sqrt{2B{E}^{2}}=\sqrt{2}BE$,故①正确;
∵DE⊥BC于E,BF⊥CD于F,
∴∠BEH=∠DEC=∠DFH=90°,
∴∠DHF+∠HDF=∠HDF+∠DCE=90°,
∴∠DCE=∠DHF,
∵∠BHE=∠DHF,四边形ABCD是平行四边形,
∴∠BAD=∠DCE,
∴∠BAD=∠BHE,故②正确
∵BE=DE,∠BEH=∠DEC=90°,∠BHE=∠DCE,
∴△BEH≌△DEC,
∴BH=CD,
又∵四边形ABCD是平行四边形,
∴AB=CD,
∴AB=BH,故③正确;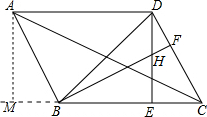 作AM⊥CB交CB的延长线于点M,如右图所示,
作AM⊥CB交CB的延长线于点M,如右图所示,
∵∠AMB=∠DEC=90°,AB=CD,AAB∥CD,
∴∠ABM=∠DCE,
∴△ABM≌△DCE,
∴BM=CE,
∴AC2+BD2=AM2+(MB+BC)2+(BE2+DE2)=DE2+(CE+BC)2+(BE2+DE2)=BC2+BE2+2BE•CE+3CE2+2DE2,
2(BC2+DC2)=BC2+BC2+2DC2=BC2+(BE+CE)2+2(DE2+CE2)=BC2+BE2+2BE•CE+3CE2+2DE2,
∴$\frac{A{C}^{2}+B{D}^{2}}{B{C}^{2}+D{C}^{2}}$=2,故④正确,
故选D.
点评 本题考查四边形综合题,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:选择题
 如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则sin∠EDB的值是( )
如图,边长为1的小正方形网格中,⊙O的圆心在格点上,则sin∠EDB的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{2}}{5}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | m+4 | B. | m+8 | C. | 2m+4 | D. | 2m+8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠NBA,BE的反向延长线与∠BAO的平分线交于点C,则∠C的度数是( )
如图,∠MON=90°,点A,B分别在射线OM,ON上运动,BE平分∠NBA,BE的反向延长线与∠BAO的平分线交于点C,则∠C的度数是( )| A. | 30° | B. | 45° | C. | 55° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 电子跳蚤游戏盘如图所示的△ABC,AB=8,AC=9,BC=10,如果跳蚤开始时在BC边的点P0处,BP0=4.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2015与A间的距离为( )
电子跳蚤游戏盘如图所示的△ABC,AB=8,AC=9,BC=10,如果跳蚤开始时在BC边的点P0处,BP0=4.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;跳蚤按上述规则一直跳下去,第n次落点为Pn(n为正整数),则点P2015与A间的距离为( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
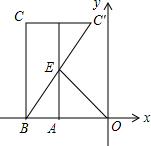 如图,已知点A的坐标为(m,0),点B的坐标为(m-2,0),在x轴上方取点C,使CB⊥x轴,且CB=2AO,点C,C′关于直线x=m对称,BC′交直线x=m于点E,若△BOE的面积为4,则点E的坐标为(-2,2).
如图,已知点A的坐标为(m,0),点B的坐标为(m-2,0),在x轴上方取点C,使CB⊥x轴,且CB=2AO,点C,C′关于直线x=m对称,BC′交直线x=m于点E,若△BOE的面积为4,则点E的坐标为(-2,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com