
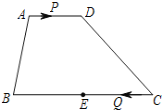
【题目】如图,四边形ABCD中,AD∥BC,AD=3,BC=8,E是BC的中点,点P以每秒1个单位长度的速度从A点出发,沿AD向点D运动;点Q同时以每秒2个单位长度的速度从点C出发,沿CB向点B运动,点P停止运动时,点Q也随之停止运动.当运动时间t=__________秒时,以点P,Q,E,D为顶点的四边形是平行四边形.
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
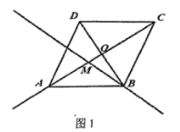
【题目】如图,![]() 为菱形
为菱形![]() 对角线的交点,
对角线的交点,![]() 是射线
是射线![]() 上的一个动点(点
上的一个动点(点![]() 与点
与点![]() ,
,![]() ,
,![]() 都不重合),过点
都不重合),过点![]() ,
,![]() 分别向直线
分别向直线![]() 作垂线段,垂足分别为
作垂线段,垂足分别为![]() ,
,![]() ,连接
,连接![]() ,
,![]() .
.
(1)①当点![]() 在线段
在线段![]() 上时,在图1中依据题意补全图形:
上时,在图1中依据题意补全图形:
②猜想![]() 与
与![]() 的数量关系为 .
的数量关系为 .
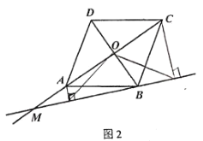
(2)小东通过观察、实验发现点![]() 在线段
在线段![]() 的延长线上运动时,(1)中的猜想始终成立.
的延长线上运动时,(1)中的猜想始终成立.
小东把这个发现与同学们进行交流,通过讨论,形成了证明此猜想的几种想法:
想法1:由已知条件和菱形对角线互相平分,可以构造与![]() 全等的三角形,从而得到相等的钱段,再依据直角三角形斜边中线的性质,即可证明猜想;
全等的三角形,从而得到相等的钱段,再依据直角三角形斜边中线的性质,即可证明猜想;
想法2:由已知条件和菱形对角线互相垂直,能找到两组共斜边的直角三角形,例如其中的一组![]() 和
和![]() ,再依据直角三角形斜边中线的性质,菱形四条边相等,可以构造一对以
,再依据直角三角形斜边中线的性质,菱形四条边相等,可以构造一对以![]() 和
和![]() 为对应边的全等三角形,即可证明猜想.
为对应边的全等三角形,即可证明猜想.
…
请你参考上面的想法,在图2中帮助小东完成画图,并证明此猜想(一种方法即可).
(3)当![]() 时,请直接写出线段
时,请直接写出线段![]() ,
,![]() ,
,![]() 之间的数量关系是 .
之间的数量关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前5名选手的得分如下:
序号 项目 | 1 | 2 | 3 | 4 | 5 |
笔试成绩/分 | 85 | 92 | 84 | 90 | 84 |
面试成绩/分 | 90 | 88 | 86 | 90 | 80 |
根据规定,笔试成绩和面试成绩分别按一定的百分比折和成综合成绩(综合成绩的满分仍为100分)
(1)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(2)求出其余四名选手的综合成绩,并以综合成绩排序确定前两名人选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知线段AB两个端点的坐标分别为A(1,-1),B(3,1),将线段AB绕点O逆时针旋转90°到对应线段CD(点A与点C对应,点B与点D对应).
(1)直接写出C,D两点的坐标;
(2)点P在x轴上,当△PCD的周长最小时,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=13 cm,AC=20 cm,BC边上的高为12 cm,则△ABC的面积是
A.126 cm2 或66 cm2B.66 cm2C.120 cm2D.126cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
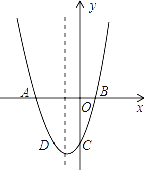
【题目】(12分)已知:二次函数y=x2+bx+c的图象与x轴交于A,B两点,其中A点坐标为(﹣3,0),与y轴交于点C,点D(﹣2,﹣3)在抛物线上.
(1)求抛物线的解析式;
(2)抛物线的对称轴上有一动点P,求出PA+PD的最小值;
(3)若抛物线上有一动点P,使三角形ABP的面积为6,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个球,其中2个红球,2个白球,它们除颜色外其余都相同.
(1)摸出1个球是白球的概率是 ;
(2)同时摸两个球恰好是两个红球的概率(要求画树状图或列表).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=100°,则∠C的度数为( )
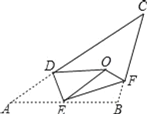
A. 40°B. 41°C. 42°D. 43°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在 Rt△ABC 中,∠ACB=90°,O为AB边上的一点,且![]() ,点D为AC边上的动点(不与点A,C 重合),将线段OD绕点O顺时针旋转90°交BC于点E.
,点D为AC边上的动点(不与点A,C 重合),将线段OD绕点O顺时针旋转90°交BC于点E.
(1)如图1,若O为AB边中点,D为AC边中点,求![]() 的值;
的值;
(2)如图2,若O为AB边中点,D不是AC边的中点,求![]() 的值。
的值。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com