
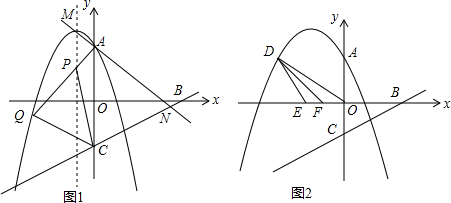
分析 (1)用抛物线的顶点公式确定顶点坐标,联立方程组求交点坐标;
(2)根据对折确定出a求出点A,C,N的坐标,从而求出三角形的面积;
(3)求出直线BC解析式为y=$\frac{\sqrt{3}}{3}$x-4$\sqrt{3}$,直线DF的解析式为y=-$\sqrt{3}$x-8$\sqrt{3}$,从而求出线段KE中点H横坐标为-3,建立方程求解.
解答 解:(1)∵y=-$\frac{\sqrt{3}}{9}$x2-$\frac{4\sqrt{3}}{3}$x+a=$\frac{\sqrt{3}}{9}$(x+6)2+a+4$\sqrt{3}$,
∴顶点M(-6,a+4$\sqrt{3}$)
令x=0,得:y=a,
∴A(0,a),
∴直线AM解析式为y=-$\frac{2\sqrt{3}}{3}$x+a,
∵$\left\{\begin{array}{l}{y=-\frac{2\sqrt{3}}{3}x+a}\\{y=\frac{\sqrt{3}}{3}x-a}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x=\frac{2\sqrt{3}}{3}a}\\{y=-\frac{1}{3}a}\end{array}\right.$,
∴N($\frac{2\sqrt{3}}{3}$a,-$\frac{1}{3}$a)
(2)由(1)知,Q(-$\frac{2\sqrt{3}}{3}$a,-$\frac{1}{3}$a),
∴-$\frac{1}{3}$a=-$\frac{\sqrt{3}}{9}$×(-$\frac{2\sqrt{3}}{3}$a)2-$\frac{4\sqrt{3}}{3}$×(-$\frac{2\sqrt{3}}{3}$a)+a,
∴a=9$\sqrt{3}$,或a=0(舍),
∴A(0,9$\sqrt{3}$),C(0,-9$\sqrt{3}$),N(-6,13$\sqrt{3}$),
∴xQ=-18,xP=-6,AC=18$\sqrt{3}$,
∴S△PQC=S△AQC-S△APC=$\frac{1}{2}$AC×|xQ|-$\frac{1}{2}$AC×|xP|=$\frac{1}{2}$×18$\sqrt{3}$(18-6)=108$\sqrt{3}$.
(3)如图,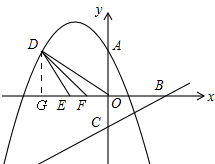
当a=4$\sqrt{3}$时,抛物线解析式为y=-$\frac{\sqrt{3}}{9}$x2-$\frac{4\sqrt{3}}{3}$x+4$\sqrt{3}$,
直线BC解析式为y=$\frac{\sqrt{3}}{3}$x-4$\sqrt{3}$,
设点K的坐标为(m,0),(m<12)
∴直线BC平移后的直线B'C'的解析式为y=$\frac{\sqrt{3}}{3}$(x-m)①,
作DG⊥x轴,
∴∠DEG=60°,
∴DG=DEsin60=4$\sqrt{3}$,EG=DEcos60°=4,
∵y=4$\sqrt{3}$,
∴4$\sqrt{3}$=-$\frac{\sqrt{3}}{9}$x2-$\frac{4\sqrt{3}}{3}$x+4$\sqrt{3}$,
∴x=-12,或x=0(舍)
∴D(-12,4$\sqrt{3}$),
∴OG=12,
∴OE=OG-EG=8,
∴E(-8,0),
∵F(-4,0),
∴直线DF的解析式为y=-$\frac{1}{2}$$\sqrt{3}$x-2$\sqrt{3}$②,
联立①②得,x=$\frac{2}{5}$(m-6),y=-$\frac{\sqrt{3}}{5}$(m+4),
∴H($\frac{2}{5}$(m-6),-$\frac{\sqrt{3}}{5}$(m+4)),
∵E(-8,0),K(m,0),
∴EK2=(m+8)2,EH2=[($\frac{2}{5}$(m-6)+8]2+[-$\frac{\sqrt{3}}{5}$(m+4)]2,HK2=[$\frac{2}{5}$(m-6)-m]2+[-$\frac{\sqrt{3}}{5}$(m+4)]2,
∵△KEH为等腰三角形,
①当EH=KH时,∴EH2=KH2,
∴[($\frac{2}{5}$(m-6)+8]2+[-$\frac{\sqrt{3}}{5}$(m+4)]2=[$\frac{2}{5}$(m-6)-m]2+[-$\frac{\sqrt{3}}{5}$(m+4)]2,
∴m=-8(舍)或m=16(舍)
②当EH=EK时,∴EH2=EK2,
∴(m+8)2=[($\frac{2}{5}$(m-6)+8]2+[-$\frac{\sqrt{3}}{5}$(m+4)]2
∴m=-4(舍)或m=-$\frac{32}{3}$,
∴K(-$\frac{32}{3}$,0),
③当KH=EK时,∴KH2=EK2,
(m+8)2=[$\frac{2}{5}$(m-6)-m]2+[-$\frac{\sqrt{3}}{5}$(m+4)]2,
∴m=$\frac{-152+40\sqrt{3}}{13}$或m=$\frac{-152-40\sqrt{3}}{13}$
∴K($\frac{-152+40\sqrt{3}}{13}$,0)或($\frac{-152-40\sqrt{3}}{13}$,0)
∴满足条件的K的坐标为(-$\frac{32}{3}$,0)或($\frac{-152+40\sqrt{3}}{13}$,0)或($\frac{-152-40\sqrt{3}}{13}$,0)
点评 此题是二次函数综合题,主要考查了图象的交点坐标的确定,锐角三角函数的意义,三角形面积的求法,解本题的关键是交点坐标的确定.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
 如图,将?ABCD沿EF折叠,点A与点C重合,点D落在点C处,若AB=6,BC=4,∠B=60°,则△CEF的面积为$\frac{7\sqrt{3}}{2}$.
如图,将?ABCD沿EF折叠,点A与点C重合,点D落在点C处,若AB=6,BC=4,∠B=60°,则△CEF的面积为$\frac{7\sqrt{3}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.5×106 | B. | 3.5×107 | C. | 35×105 | D. | 0.35×108 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
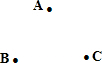 如图,点A,B,C不在同一直线线上.请利用圆规和直尺按下列要求作图(保留作图痕迹,不写作法).
如图,点A,B,C不在同一直线线上.请利用圆规和直尺按下列要求作图(保留作图痕迹,不写作法).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 四川广电网络客户服务热线为96655,这五个数的众数为5和6 | |
| B. | 了解我市学生的视力情况,适宜采用抽样调查 | |
| C. | 要了解比赛选手之间成绩的稳定性,通常比较选手比赛成绩方差的大小 | |
| D. | 扇形统计图便于显示每部分扇形所对应圆心角大小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com