
����Ŀ��1.����ѧϰ.��֪![]() ����
����![]() Ϊ���ڲ�һ�㣬����
Ϊ���ڲ�һ�㣬����![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ��
��![]() �У��������һ�������Σ����ڽ���
�У��������һ�������Σ����ڽ���![]() �������ڽǷֱ���ȣ���ô�ͳƵ�
�������ڽǷֱ���ȣ���ô�ͳƵ�![]() Ϊ
Ϊ![]() �ĵȽǵ�.
�ĵȽǵ�.

2.����Ӧ��
(1)�ж��������������Ƿ�Ϊ����⣬��Ϊ�����⣬������Ӧ������д��������������֮����д����������.
���ڽǷֱ�Ϊ![]() ��
��![]() ��
��![]() �������δ��ڵȽǵ㣻 ��
�������δ��ڵȽǵ㣻 ��
������������ζ����ڵȽǵ�; ��
��2����ͼ�٣���![]() �����
�����![]() �ĵȽǵ㣬��
�ĵȽǵ㣬��![]() ��̽��ͼ���У�
��̽��ͼ���У�![]() ��
��![]() ��
��![]() ֮���������ϵ����˵������.
֮���������ϵ����˵������.
3.�������
��ͼ�ڣ���![]() �У�
��![]() ����
����![]() �������ڽǵĽ�ƽ���ߵĽ���
�������ڽǵĽ�ƽ���ߵĽ���![]() �Ǹ������εĵȽǵ㣬��
�Ǹ������εĵȽǵ㣬��![]() �����������ڽǵĶ���.
�����������ڽǵĶ���.
���𰸡���1���棬�٣���2����BPC����ABC����ACP��֤����������3��![]() ��
��![]() ��
��![]() ��
��
��������
��1�����ݵȽǵ�Ķ��壬��֪�ڽǷֱ�Ϊ30��60��90�������δ��ڵȽǵ㣬���ȱ������β����ڵȽǵ㣬�ݴ��жϼ��ɣ�
��2�����ݡ�ABC�У���BPC����ABP����BAC����ACP�Լ���BAC����PBC�����Ƶ������ɵó���BPC����ABC����ACP֮���������ϵ��
��3�����ݡ�ABC�������ڽǵĽ�ƽ���ߵĽ���P�Ǹ������εĵȽǵ㣬�Լ��������ڽǺ�Ϊ180�㣬�ó����ڡ�A�ķ��̣���á�A�Ķ������ó��������������ڽǵĶ�����
�⣺��1�����ڽǷֱ�Ϊ30��60��90�������δ��ڵȽǵ��������⣻
������������ζ����ڵȽǵ��Ǽ����⣬��ȱ������β����ڵȽǵ㣻
�ʴ�Ϊ���棬�٣�
��2����BPC����ABC����ACP���������£�
��ͼ�٣�
���ڡ�ABC�У���BPC����ABP����BAC����ACP����BAC����PBC��
���BPC����ABP����PBC����ACP����ABC����ACP��
��3����PΪ��ABC�Ľ�ƽ���ߵĽ��㣬
���PBC��![]() ��ABC����PCB��
��ABC����PCB��![]() ��ACB��
��ACB��
��PΪ��ABC�ĵȽǵ㣬
���PBC����BAC����BCP����ABC��2��PBC��2��BAC����ACB����BPC��4��A��
�֡ߡ�A����ABC����ACB��180�㣬
���A��2��A��4��A��180�㣬
���A��![]() ��
��
��������������ڽǵĶ����ֱ�Ϊ![]()
![]()
![]() ��
��


 �Ǽ�����������ϵ�д�
�Ǽ�����������ϵ�д� â���̸������Ծ�ϵ�д�
â���̸������Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AD�ǡ�ABC�Ľ�ƽ���ߣ�DE��AC������ΪE��BF��AC��ED���ӳ����ڵ�F����BCǡ��ƽ�֡�ABF��AE��2BF�����������ĸ����ۣ���DE��DF����DB��DC����AD��BC����AC��3BF��������ȷ�Ľ��۹��У�������
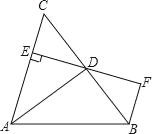
A. �٢ڢۢ� B. �٢ڢ� C. �٢ڢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC=120����BD ƽ�֡�ABC����DAC=60������ AB=2��BC=3���� BD=_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
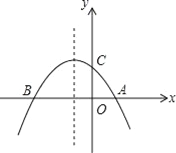
����Ŀ����ͼ����֪������y=��![]() x2��
x2��![]() x+2��x�ύ��A��B���㣬��y�ύ�ڵ�C
x+2��x�ύ��A��B���㣬��y�ύ�ڵ�C
��1�����A��B��C�����ꣻ
��2����E�Ǵ��������ϵĵ㣬��F����Գ����ϵĵ㣬����A��B��E��FΪ�����ƽ���ı��ε������
��3���������ߵĶԳ������Ƿ���ڵ�M��ʹ����ACM�ǵ��������Σ������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
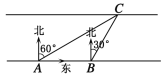
����Ŀ����ͼ���ס��������ڵ�·������������У����ס������˷ֱ�������A��Cʱ��������ڼı�ƫ��60�㷽������������ԭ����Ϣ��������ǰ����40��B������ʱ��������䱱ƫ��30�㷽���������·�Ŀ����ο����ݣ�![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪ AD �ǡ�ABC �ı� BC �ϵ����ߣ�
��1��������ABD �ı� BD �ϵĸߣ�
��2������ABC �����Ϊ 10�����ADC �������
��3������ABD �����Ϊ 6���� BD ���ϵĸ�Ϊ 3���� BC �ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
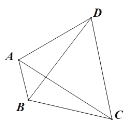
����Ŀ����ͼ���������������ϵ����AD��BC����AC��BD����CE��DE���ܡ�D����C���ݡ�DAB����CBA��

��������������Ϊ���������������е�һ��Ϊ���ۣ��Ƴ�һ����ȷ�Ľ��ۣ�ֻ��д��һ���������������֤����
��֪��
��֤��
֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
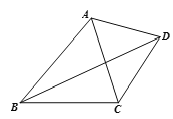
����Ŀ����ͼ����֪���ı���ABCD�У��Խ���BDƽ�֡�ABC����DCB=123������ABC=50�������ҡ�BAD+��CAD=180������ô��DAC�Ķ���Ϊ_________��.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com