
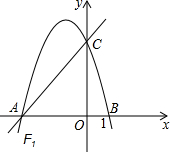
 ��ͼ��ֱ��y=$\frac{4}{3}$x+4����x���ڵ�A����y���ڵ�C����A��C�����������F1��x������һ��B��1��0����
��ͼ��ֱ��y=$\frac{4}{3}$x+4����x���ڵ�A����y���ڵ�C����A��C�����������F1��x������һ��B��1��0�������� ��1������õ�A�͵�C�����꣬��������F1�Ľ���ʽΪ��y=a��x+3����x-1������C��0��4����������a��ֵ��
��2��ȡ��B����y��ĶԳƵ�B�䣨-1��0��������CB�䣬���BCO=��B��CO����ֱ��B��C�Ľ���ʽΪy=kx+b������B��͵�C�������������ֱ��B��C�Ľ���ʽ����y=4x+4��y=-$\frac{4}{3}$x2-$\frac{8}{3}$x+4����õ�P�����ꣻ
��3������CMN=90��ʱ��ֱ��MN�Ľ���ʽΪy=-$\frac{3}{4}$x-6����y=$\frac{4}{3}$x+4��y=-$\frac{3}{4}$x-6���������M�����ꣻ����CNMΪֱ��ʱ��MN��x�ᣬ��y=-6����y=$\frac{4}{3}$x+4����õ�M�ĺ����꣮
��� �⣺��1����y=0����y=$\frac{4}{3}$x+4����ã�x=-3��
��A��-3��0����
��x=0������y=$\frac{4}{3}$x+4����y=4��
��C��0��4����
��������F1�Ľ���ʽΪ��y=a��x+3����x-1����
��C��0��4��������ʽ�ã�a=-$\frac{4}{3}$��
��y=-$\frac{4}{3}$x2-$\frac{8}{3}$x+4��
��y=-$\frac{4}{3}$��x2+2x+1��+$\frac{20}{3}$��
��Q��-1��$\frac{20}{3}$����
��2���ߵ�B������Ϊ��1��0����ȡ��B����y��ĶԳƵ�B�䣨-1��0��������CB�䣬���BCO=��B��CO��
���BPC��������y���ϣ�
��ֱ��B��C�Ľ���ʽΪy=kx+b������B��͵�C���������ã�$\left\{\begin{array}{l}{b=4}\\{-k+b=0}\end{array}\right.$��
��ã�k=4��b=4��
��ֱ��B��C�Ľ���ʽΪy=4x+4��
��y=4x+4��y=-$\frac{4}{3}$x2-$\frac{8}{3}$x+4�����ã�$\left\{\begin{array}{l}{y=4x+4}\\{y=-\frac{4}{3}{x}^{2}-\frac{8}{3}x+4}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=-5}\\{y=-16}\end{array}\right.$��$\left\{\begin{array}{l}{x=0}\\{y=4}\end{array}\right.$����ȥ����
���P��������-5��-16����
��3��N��0��-6����ֱ��AC�ı���ʽΪy=$\frac{4}{3}$x+4��
����MNC�ס�AOCʱ����CMN=90�㣮
��ֱ��MN��һ����ϵ��Ϊ-$\frac{3}{4}$��
��MN�Ľ���ʽΪy=-$\frac{3}{4}$x-6��
��y=$\frac{4}{3}$x+4��y=-$\frac{3}{4}$x-6��������ã�$\left\{\begin{array}{l}{x=-\frac{24}{5}}\\{y=-\frac{14}{5}}\end{array}\right.$��
���M��������-$\frac{24}{5}$��-$\frac{14}{5}$����
�ڵ���CNMΪֱ��ʱ��MN��x�ᣬ
��y=-6����y=$\frac{4}{3}$x+4�ã�$\frac{4}{3}$x+4=-6����ã�x=-$\frac{15}{2}$��
��M��-$\frac{15}{2}$��-6����
������������M��������-$\frac{24}{5}$��-$\frac{14}{5}$����-$\frac{15}{2}$��-6����
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˴���ϵ������һ�κ��������κ����Ľ���ʽ�����������ε��ж��������ε����ģ����������ǽ���Ĺؼ���


 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
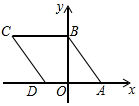 ��ͼ���ı���ABCD�����Σ�A��3��0����B��0��4�������C�������ǣ�-5��4����
��ͼ���ı���ABCD�����Σ�A��3��0����B��0��4�������C�������ǣ�-5��4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=8��x+2010��2+2011 | B�� | y=8��x-2010��2+2011 | ||
| C�� | y=-8��x-2010��2-2011 | D�� | y=-8��x+2010��2+2011 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
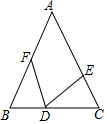 ��ͼ���ڡ�ABC�У���B=��C��BD=CE��CD=BF�����EDF���ڣ�������
��ͼ���ڡ�ABC�У���B=��C��BD=CE��CD=BF�����EDF���ڣ�������| A�� | 90��-��A | B�� | 90��-$\frac{1}{2}$��A | C�� | 180��-2��A | D�� | 45��-$\frac{1}{2}$��A |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com