
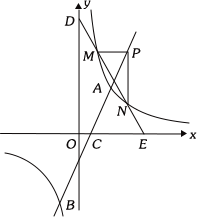
����Ŀ����ͼ��ֱ��y=ax+b(a��0)��˫����![]() (k��0)����һ���������ڵ�A��B������x�ύ�ڵ�C����A������Ϊ(2��m)����B������Ϊ(1��n)��cos��AOC=
(k��0)����һ���������ڵ�A��B������x�ύ�ڵ�C����A������Ϊ(2��m)����B������Ϊ(1��n)��cos��AOC=![]() .
.
(1)��÷�����������һ�κ����Ľ���ʽ��
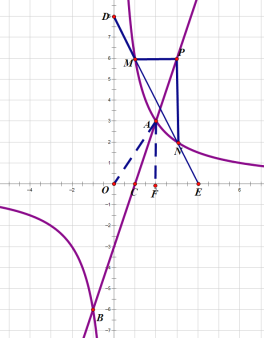
(2)��QΪy����һ�㣬��ABQ����ABΪֱ�DZߵ�ֱ�������Σ����Q�����ꣻ
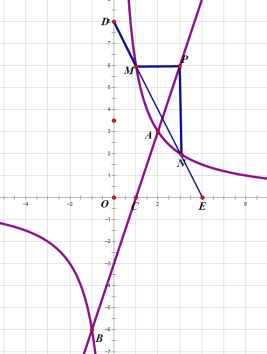
(3)��P(s��t)(s>2)��ֱ��AB���˶���PM��x�ύ˫������M��PN��y�ύ˫������N��ֱ��MN�ֱ�x�ᣬy����E��D����![]() ��ֵ.
��ֵ.
���𰸡���1��![]() ��
��![]() ��2��Q��0��
��2��Q��0��![]() ����0��
����0��![]() ����3��1
����3��1
��������
(1)����AO������![]() ����A������Ϊ2�����Եó���A�������꣬��A��������뷴���������Ϳɵó������ʽ,���A��B����ֱ����һ�κ��������һ�κ�������ʽ��
����A������Ϊ2�����Եó���A�������꣬��A��������뷴���������Ϳɵó������ʽ,���A��B����ֱ����һ�κ��������һ�κ�������ʽ��
(2)���ݵ�Q��y��������������������ȥ����ֱ�������ν����ڹ��ɶ��������Q���꼴�ɣ�
(3)�����������M��N������ֱ���s��t��ʾ��Ȼ�����PM��PN�ij�������![]() ���������.
���������.
�⣺(1)����AO������![]() ����A������Ϊ2��
����A������Ϊ2��
�ã�![]() ,��
,��![]() ,
,
����![]() ��������뷴��������ʽ
��������뷴��������ʽ
![]()
![]() ��������
��������![]() ��
��
��![]() ��
��![]() �������һ�κ�������ʽ��
�������һ�κ�������ʽ��![]()
![]() ����ã�
����ã�![]() ��
��
![]() .
.
(2)��ͼ��ʾ��
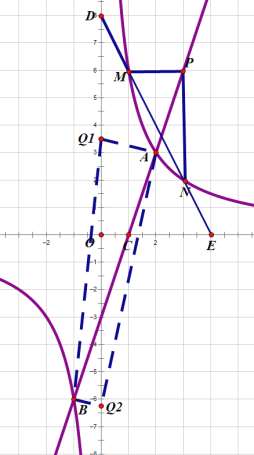
�ٵ���![]() λ��y���������ʱ��
λ��y���������ʱ��
��ʱ![]()
����![]()
��ã�![]() ��
��
![]() ��
��
�ڵ���![]() λ��y�Ḻ�����ʱ��
λ��y�Ḻ�����ʱ��
��ʱ![]()
����![]()
��ã�![]() ��
��
![]() ��
��
�ۺϵã�![]() ��
��![]() .
.
(3)��������ɵã�![]() ��
��
��![]() ����
����![]() ��
��
������![]() ��
��![]() ��
��
![]() ��
��
����P��ֱ��![]() ������
������![]() ��
��
���߳���t�ã�![]() ��
��
�ۺ������ɵã�![]() ��
��
�ʴ�Ϊ��1


 ����ͬ�����Ծ�ϵ�д�
����ͬ�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������![]() ��
��![]() ��ֱ��l��
��ֱ��l��![]() ����x���ϵ�һ��A������һ��
����x���ϵ�һ��A������һ��![]()

![]() ��������
��������![]() �Ľ���ʽ��
�Ľ���ʽ��
![]() ��P��������
��P��������![]() �ϵ�һ������
�ϵ�һ������![]() ��P��A��B����֮�䣬��������A��B����
��P��A��B����֮�䣬��������A��B����![]() �ڵ�M��
�ڵ�M��![]() �ύAB�ڵ�N����MN�����ֵ��
�ύAB�ڵ�N����MN�����ֵ��
![]() ��ͼ2����������
��ͼ2����������![]() �ƶ�����ת
�ƶ�����ת![]() �������ʵ�ƽ�Ƶõ�������
�������ʵ�ƽ�Ƶõ�������![]() ����֪������
����֪������![]() �Ķ���E�ڵ�һ����������
�Ķ���E�ڵ�һ����������![]() �ϣ����׳���
�ϣ����׳���![]() ��������
��������![]() ���ڵ�D������D��
���ڵ�D������D��![]() �ύ������
�ύ������![]() �ڵ�F������E��
�ڵ�F������E��![]() �ύ������
�ύ������![]() �ڵ�G���Ƿ����������������
�ڵ�G���Ƿ����������������![]() ��ʹ���ı���DFEGΪ���Σ������ڣ�����E��ĺ����ꣻ�������ڣ���˵�����ɣ�
��ʹ���ı���DFEGΪ���Σ������ڣ�����E��ĺ����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
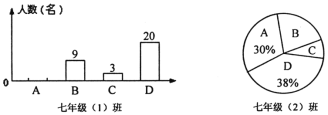
����Ŀ������ǵø�ĸ�������𣿡�����ij��ѧ�����꼶ѧ���п�չ����Ϊ���ж�������ʱ ���õ�һ�����⣬�������ĸ�ѡ�A����ĸ���ն��ǵã�B��ֻ�ǵ�ĸ�����գ�C��ֻ �ǵø������գ�D����ĸ���ն����ǵã�����������ˣ�1����ͣ�2����� 50 ��ѧ ������������ݻ����ͼ��ʾ��ͳ��ͼ��
��1����ȫƵ���ֲ�ֱ��ͼ��
��2����֪��У���꼶�� 900 ��ѧ�����ݴ����㣬��У���꼶ѧ���У�����ĸ���ն� ���ǵá���ѧ������������
��3�����������С�ֻ�ǵ�ĸ�����ա���ѧ��ռ 22������2���ࡰֻ�ǵ�ĸ�����ա� ��ѧ����ռ�ٷֱ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ֪��l��y����x+4�ֱ���x�ᡢy�ύ�ڵ�A��B��˫����![]() ��k��0��x��0����ֱ��l���ཻ��EΪ˫������һ���㣬����E��EG��x���ڵ�G��EF��y���ڵ�F���ֱ���ֱ��l���ڵ�C��D���ҡ�COD��45�㣬��k��_____��
��k��0��x��0����ֱ��l���ཻ��EΪ˫������һ���㣬����E��EG��x���ڵ�G��EF��y���ڵ�F���ֱ���ֱ��l���ڵ�C��D���ҡ�COD��45�㣬��k��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ4��������ABCD�У�E��F�ֱ�ΪBC��CD���е㣬����AE��BF���ڵ�G������BCF��BF���ۣ��õ���BPF���ӳ�FP��BA�ӳ����ڵ�Q�����������ĸ����ۣ�
��QB=QF����BG=![]() ����tan��BQP=
����tan��BQP=![]() ����S�ı���ECFG=2S��BGE��������ȷ����_______.
����S�ı���ECFG=2S��BGE��������ȷ����_______.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��ȤС��Ϊ������ͼ������ʾ��һ�ιų�ǽ�ĸ߶ȣ������ƽ�澵������ʾ��ͼ��ͼ����ʾ����P����һˮƽ��ƽ�澵�����ߴӵ�A��������ƽ�澵�����պ��䵽�ų�ǽCD�Ķ���C����

��1����֪AB��BD��CD��BD���Ҳ��AB=1.2m��BP=1.8m.PD=12m����ó�ǽ�ĸ߶ȣ�ƽ�澵��ԭ�Ⱥ��Բ��ƣ���
��2���������һ��������ιų�ǽ�߶ȵķ�����
Ҫ�����ʾ��ͼ����Ҫ��д����������д��������������Ҫ�ļ�����̣��۸����ķ��������õ�ͼ�ڵķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�ǵȱ������Σ�AB=4��E��AC���е㣬D��ֱ��BC��һ���㣬�߶�ED�Ƶ�E��ʱ����ת90�����õ��߶�EF������D�˶�ʱ����AF����СֵΪ�� ��
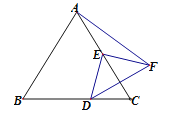
A.2B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Rt��ABC�У�DΪб��AB���е㣬��B=60�㣬BC=2cm������E�ӵ�A������AB���B�˶�������F�ӵ�D������������D��C��B�˶���������ٶȾ�Ϊ1cm/s�������յ��ֹͣ�˶�����AE�ij�Ϊx����AEF�����Ϊy����y��x��ͼ�����Ϊ��������

A.  B.
B. 
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ2����E��F�ֱ��ڱ�AD��CD�ϣ�����EBF��45��������EDF���ܳ����ڣ�������
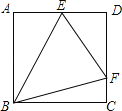
A.2![]() B.3C.4D.4
B.3C.4D.4![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com